Placenta protectors no match for toxic Strep B pigment
Bacterial weapon pokes holes in immune cells, study in monkeys shows
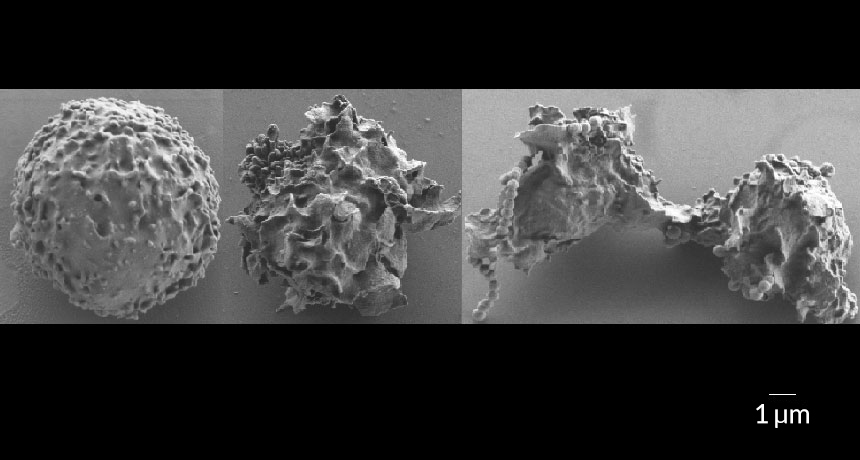
MICROBIAL MACHETE A toxic pigment made by Strep B bacteria destroys infection-fighting cells called neutrophils (healthy neutrophil, left; one exposed to a pigmented strain of Strep B, middle; one exposed to a hyperpigmented strain, right).
Boldenow et al/Science Immunology 2016
A type of bacteria that can cause stillbirth and fatal illness in newborns attacks with an unlikely weapon: an orange pigment made of fat.
This pigment mutilates infection-fighting immune system cells, enabling the bacteria — Group B Streptococcus — to quickly cross the placenta and invade the amniotic sac, a new study in monkeys shows. In one case, it took as little as 15 minutes for the bacteria to cross the protective membrane, researchers report October 14 in Science Immunology.
“That’s shocking,” says study coauthor Kristina Adams Waldorf, a specialist in obstetrics and gynecology at the University of Washington in Seattle. “The poor placenta has no time to control the invasion.”
Strep B bacteria are an often harmless part of the gastrointestinal tract and vaginal flora of healthy women. But during pregnancy, the bacteria can cause serious problems, including preterm labor, stillbirth and life-threatening infections.
Previous work led by study coauthor Lakshmi Rajagopal, a microbiologist at Seattle Children’s Research Institute and the University of Washington, found that strains of Strep B isolated from the amniotic fluid of women who went into preterm labor made an orange pigment. Experiments in lab dishes revealed that these pigmented strains were especially good at invading the placenta. But experiments with placental tissue in the lab are often muddied by antibiotics taken by the mother during labor to prevent passing an infection to her baby. And researchers don’t want to conduct invasive tests on pregnant women that could reveal more about such infections. So it was unclear how Strep B infections progressed or how neutrophils, the mother’s immune system cells, responded to the pigment-wielding bacteria.
“Neutrophils are the first line of defense,” says Adams Waldorf. “If a placenta can’t rely on its neutrophils to get rid of infection, it’s really in trouble.”
The researchers studied the progression of infection in macaques, whose pregnancy closely mimics human pregnancy. Ten pregnant monkeys got a strain of Strep B that makes a lot of pigment or a strain that couldn’t make the pigment. (Five additional monkeys got saline solution as a control.)
Two monkeys in the group exposed to pigment-free Strep B had problematic pregnancies. But pregnancies in all the monkeys exposed to pigmented Strep B had problems. Four went into early preterm labor; the fifth had an emergency C-section after researchers found discolored amniotic fluid indicating an infection.
Pathogen-fighting neutrophils flooded the site of infection, but to no avail, the researchers found. Strep B’s pigment, a long chain of fat attracted to cell membranes, quickly poked holes in the neutrophils. Unlike some bacterial weaponry, the pigment “doesn’t make a nice defined hole,” says Rajagopal. “It inserts in random places, disfiguring the membrane.” Neutrophils are known to expel their innards, ensnaring invaders in a mess of DNA and chromatin, but those traps were ineffective against the pigment.
“This is a beautiful, elegant study,” says Maria Gloria Dominguez-Bello of the New York University School of Medicine. The work raises lots of questions, such as how Strep B can go from harmless to dangerous. “Why can we live with such a potential enemy? And how can we avoid the virulent strains?” Dominguez-Bello asks.
Other recent work found that some strains of Strep B emit toxic fluid-filled sacs that are associated with stillbirth in mice (SN: 10/01/16, p. 11), but the pigment seems to be the bacteria’s primary weapon. The discovery suggests vaccine developers need to rethink their strategies, says Rajagopal.
Current Strep B vaccines in development don’t take into account the presence or absence of the toxic pigment. Doing that will be a challenge, Rajagopal says. Most vaccines are made with proteins; the fatty pigment chain isn’t soluble in water, making it difficult to work with. “First we have to make enough that we can tinker with it,” she says. “It’s tricky.”
Editor’s note: This story was updated October 24, 2016, to correct the outcome results of the monkeys given a pigment-free version of Strep B.
