Making Data Work

A fundamental problem for almost all science is how to tell a fluke from a fact.

It’s usually very hard to know whether an experiment’s result reflects a truth of nature or a random accident. So scientists use elaborate math to gauge the odds that a finding is bogus. But those odds rarely offer definitive evidence — or even much evidence at all. In fact, evidence in science is a slippery concept. It’s kind of like the U.S. Supreme Court’s idea of pornography: Scientists supposedly know evidence when they see it.

But they don’t know precisely how much evidence they’ve got; standard mathematical tricks for drawing inferences do not translate statistical data into a quantitative measure of evidential weight. Whether assessing the cancer risk from a food additive, the curative power of a new medicine or the results of an athlete’s drug test, evidence pro and con cannot be easily quantified, compared or objectively added up. For today’s scientists, weighing evidence is like measuring temperature before the invention of the thermometer.

For that matter, primitive thermometers didn’t do such a hot job either. Not until the mid-19th century, when British physicist Lord Kelvin invented the absolute temperature scale, could scientists speak accurately about how much hotter one object was than another. Kelvin derived his temperature definition using the nascent science of thermodynamics — the laws of nature governing the flow of heat. With a firm theory relating heat flow, volume, pressure and temperature, he could define a temperature scale where zero meant the absence of heat and each degree represented the same amount of temperature difference. Modern scientists trying to “take the temperature” of their evidence desperately need a similarly rigorous scale.

So contends Veronica Vieland, a statistical geneticist at the Battelle Center for Mathematical Medicine at Nationwide Children’s Hospital and Ohio State University in Columbus. In several articles published during recent years, she has trumpeted the need for a better measure of evidence — a way to gauge the reliability of data linking genes to disease, for instance.

With Susan Hodge, also of the Battelle Center, and other collaborators, Vieland has proposed that something like Kelvin’s temperature scale could serve as the model for calibrating the strength of evidence in biomedical research.

“The more I pursued the analogy,” says Vieland, “the more I started to think that our problem wasn’t just like Kelvin’s problem, it actually is Kelvin’s problem.”

Now she and her colleagues have produced a paper, recently posted online (arxiv.org/abs/1206.3543), that outlines the temperature-evidence analogy in detail. Equations transliterated from thermodynamics to statistical data show how the weight of evidence can be assessed on an absolute scale, at least for a simple standard example: whether a coin is balanced fairly for flipping.

If you flip a penny 10 times and get four heads, it’s not obvious whether the coin was doctored to favor tails. Insights from probability math show that four heads out of 10 makes for very weak evidence (if any at all) that a coin is biased. But nobody has ever devised a very clear way to quantify that evidence. A standard statistical measure, called the P value, supposedly tells you how likely you are to get four heads (or fewer) out of 10 flips if the coin is fair. But that’s not the same as evidence that the coin is or isn’t fair — a P value is merely the probability that data are consistent with the hypothesis being tested. P values alone cannot quantify the probability of the hypothesis itself.

All sorts of problems afflict P values (SN: 3/27/10, p. 26); they are not a calibrated unit of measurement — that is, they mean different things in different contexts — and in general they don’t behave like evidence is supposed to behave, as Hodge emphasized at a recent workshop in Columbus. “P values depend on decisions made by investigators,” she said. Precisely the same data can be assigned different P values, for instance, depending on seemingly irrelevant considerations, such as whether the experimenter had planned to flip the coin 10 times, or to flip it until four heads showed up.

And as Vieland notes, it wouldn’t make sense to add strong evidence to weak evidence and conclude that the total evidence is lukewarm. But that’s what P values typically do. So P values do not measure evidence in any standard way. Before Kelvin, the same was true for temperature measurements.

Warming up to statistics

At first glance, temperature and heat don’t seem to have much to do with statistics and evidence. But after a bit of reflection, Vieland’s idea makes some sense. Temperature, after all, is itself a statistical concept. In a gas of a given temperature, the molecules fly around at a wide range of speeds; the measured temperature is related to the average velocity of the molecules.

Scientific evidence, like temperature, is also usually statistical. Evidence is typically presented as a statistical analysis of data gathered in an experiment, often expressed as a P value. But unlike P values, temperature measures the same thing regardless of substance or circumstance.

Producing the evidence version of the Kelvin temperature scale requires translating thermodynamics math into analogous equations for evidence. Doing so draws on earlier work relating thermodynamics to information theory. Information theory measures a quantity of information, designated entropy, with precisely the same math used in computing the entropy described by the second law of thermodynamics.

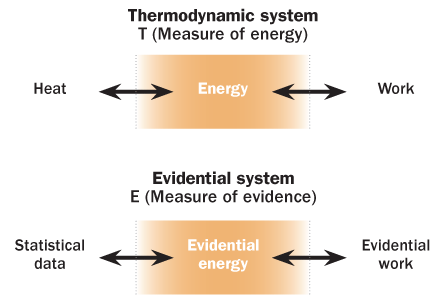
Using this mathematical connection between thermodynamic entropy and information entropy, Vieland and colleagues show how to treat statistical data as a gas governed by the laws of thermodynamics. In thermodynamics, an “equation of state” describes how the pressure and volume of a gas relate to its temperature. Vieland and colleagues rewrite the equation to describe statistical data that test whether a coin is fair. Results from sets of coin tosses (number of heads per number of flips) are the units of data, corresponding to molecules in a gas. In the new equation, temperature (T) of a gas is replaced by E, a measure of strength of evidence or “evidential energy.” Volume becomes the quantity of statistical data; pressure becomes a measure of how much changing the amount of statistical data affects the evidential energy.

With this analogy, statisticians could plot data in a way that shows how the strength of the evidence varies for competing hypotheses (the coin is fair, or the coin is biased). A key point is that the new evidence measure can be calibrated on an absolute scale (like Kelvin’s temperature), so that new data (from more coin flipping) can adjust the evidence plot in a consistent way.

Vieland describes that process as the flow of “evidential information,” analogous to the flow of heat in a steam engine (as governed by the laws of thermodynamics).

Math for describing such heat flow was worked out in the early 19th century by the French savant Sadi Carnot. His goal was figuring out how to make steam engines efficient — maximizing the work that could be done with a given amount of heat. In a typical engine, heat expands a gas (say, in a piston). As the gas expands, the pressure in the piston gets lower. And after the heat input stops, the gas cools but continues to expand, doing work. To start the cycle over, work is needed to push the piston downward, compressing the gas and raising its pressure. Engines are useful because more work comes out in the first part of the cycle than is needed to restore the piston to its starting position. And thermodynamics is useful for describing such engines because the ratio of work output to input depends solely on temperature and not on the substance being heated (the insight that allowed Kelvin to develop the absolute temperature scale).

Vieland and friends work out the coin analogy in terms of the Carnot cycle; her informational steam engine shows how the flow of information (in a set of statistical data) relates to E, the evidence equivalent of temperature. “A given change in evidential energy will always correspond to the same amount of change in E,” Vieland and colleagues write.

Pursuing the analogy a little further, Vieland suggests a “first law” of evidence: “conservation of total evidential information,” in parallel with the conservation of energy. In this case, the information law states that evidence cannot be expanded without additional input of data. Evidence’s analog to thermodynamics’ second law would be something like “evidence flows in only one direction” — that is, data used once cannot be reused, just as waste heat from an engine cannot create order but merely contributes to rising entropy, or disorder.

Beyond fair coin flipping

While this work demonstrates a way of measuring evidence in principle, much more work needs to be done, Vieland emphasizes.

“We have not so much solved the evidence measurement problem, as reformulated it in a way that makes it amenable to solution for the first time,” Vieland writes in her paper with Hodge, Jayajit Das and Sang-Cheol Seok. “Our formalism would not replace other statistical investigations, but it would ideally provide a basis for reporting results of statistical analyses on a unified scale for purposes of meaningful comparison … across disparate applications.”

At the Columbus workshop, convened to discuss issues of measurement theory in biology, other experts expressed interest in the Vieland proposal. They agreed that the problem of measuring evidence in biology is deep; biological data analysis commonly lacks the theoretical underpinnings needed to guarantee validity. A whole field of theoretical study known as measurement theory, designed to address such issues, goes largely ignored.

“There is very little discussion of measurement theory in biology,” said Thomas Hansen of the University of Oslo. “That has unfortunate consequences.”

Hansen and others wondered, though, whether the thermodynamics analogy is necessary to address the problem. If a measurement system inspired by thermodynamics turns out to work, fine, but the motivating analogy does not need to be included in justifying a new system of measuring evidence, they suggested.

But Vieland thinks something more fundamental is going on than a dispensable analogy. “This is more than an analogy — there really is reason to think that we have a system that works like a thermodynamic system at least to some extent,” she says. “I actually think we are underestimating the connection between the mathematics of thermodynamics and the mathematics of information flow and dynamical information systems. I think there is a deep mathematical connection.”

In the past, efforts to connect information to thermodynamics have often been casually dismissed. Although entropy in information theory and entropy in thermodynamics are described by the same math, traditionally most physicists have treated that curiosity as a mere coincidence. But more recently, some physical findings have suggested that the link between information and thermodynamic entropy is deep. Black hole physics, for instance, profited enormously from work by Stephen Hawking and others linking the physical entropy of black holes with the amount of information they have swallowed. Further work has merged physics with information more generally in the study of quantum information theory (SN: 4/7/12, p. 26).

As physics Nobel laureate Frank Wilczek writes in a recent paper (arxiv.org/abs/1204.4683), analogies comparing thermodynamics to information have been around for decades. At first, such analogies seemed limited, “because on the information side there did not appear to be richness of structure comparable to what we need on the physical side. Recent developments in quantum information theory have, however, unveiled a wealth of beautiful structure,” with “profound, natural connections to just that structure.”

So it may well be that the reach of thermodynamics really does extend from steam engines, black holes and information theory to the quantification of the weight of evidence in all sorts of realms. If so, biology and other sciences would surely benefit.

“I have to think that there are just major errors going on out there,” Vieland says. “We’re just misinterpreting data in a way that’s completely obscure to biologists. Biologists have no way of seeing what these errors might be or when they might be happening.” It would be nice if curing that problem could be a simple as taking a temperature.

Tom Siegfried is the former Editor in Chief of Science News.