This blog is dead. Long live the blog.
Blogs are synonymous with the early internet. But what is a blog, and what has it become? A blog is a platform. And this one, Scicurious, is now gone.
Scicurious
A peek behind the science curtain
We summarize the week's scientific breakthroughs every Thursday.
More Stories in Scicurious
- Science & Society
Women and men get research grants at equal rates — if women apply in the first place
When women get research funding, they’ll stay funded as long as their male counterparts. But getting to the top of that heap is a challenge.
- Science & Society
Fighting sexual harassment in science may mean changing science itself
Sexual harassment is disturbingly prevalent in academia. But a course correction may involve tearing down the hierarchy that makes science run.
- Health & Medicine
To regulate fecal transplants, FDA has to first answer a serious question: What is poop?
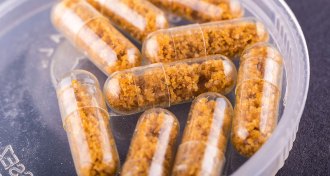
Fecal transplants are the treatment of the future for some conditions. But right now, they are entirely unregulated. Here’s why putting regulations in place is so complex.
- Chemistry
Want to build a dragon? Science is here for you
Fire-breathing dragons can’t live anywhere outside of a book or TV. But nature provides some guidance as to how they might get their flames. If they existed, anyway.
- Science & Society
Wikipedia has become a science reference source even though scientists don’t cite it
Wikipedia is everyone’s go-to source. Even scientists. A new study shows how science on Wikipedia may end up forwarding science itself.
- Neuroscience
Even brain images can be biased
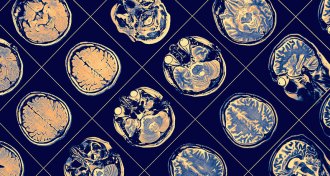
Brain scan studies that are drawn from rich and well-educated groups could lead to biased ideas of how our brains develop.
- Psychology
Whether psychology research is improving depends on whom you ask
Psychologists are pessimistic about the state of their field but want to improve, a survey shows. But are new measures working?
- Genetics
Two artificial sweeteners together take the bitter out of bittersweet
Some artificial sweeteners are well known for their bitter aftertastes. But saccharin and cyclamate are better together, and now scientists know why.
- Science & Society
On social media, privacy is no longer a personal choice
Data from the now-defunct social platform Friendster show that even people not on social media have predictable qualities.
