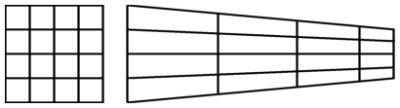

The practice of laying a grid on top of a drawing, then painstakingly copying each line of the drawing to the corresponding cell of a blank grid seems old-fashioned in these days of pervasive photocopying and electronic image manipulation.
Nonetheless, the underlying idea of transferring information from one grid to another has a long history in both mathematics and art. When the blank grid differs from the original grid, for example, a drawing can suffer intriguing distortions. In art, the result is sometimes called an anamorphic picture. Mathematically, you’re looking at the results of a type of transformation or mapping.
To create one sort of anamorphic picture, you start with a piece of paper ruled into square cells and another ruled with the same number of trapezoids. Draw your picture on the square grid. Then carefully copy the contents of each square of the original grid to the corresponding trapezoid of the other grid, stretching the lines of the drawing to make sure everything fits together. You end up with a distorted version of the original picture. Interestingly, if you now look at the final drawing at the proper angle from the edge, it appears undistorted.
You’ve probably experienced the same effect while riding in a car and encountering the word “STOP” painted on the roadway just before an intersection. The white letters look normal from where you are sitting. If you were standing beside the sign instead of riding toward it, however, you would find that the letters are actually stretched out.
Artists have long used the same idea to create visual puzzles. In such examples, a viewer sees an object correctly only if he or she finds the right angle at which to look at the picture. One of the most famous examples is in a painting called “The Ambassadors,” made by the German artist Hans Holbein, the Younger (1497-1543). It shows two men standing in front of tables overflowing with books, instruments, and globes (see http://www.mezzo-mondo.com/arts/mm/holbein/HOH006.html). At their feet, the artist painted a weird shape that turns out to be a grinning skull when you hold the picture at a slant and view it in the right way.
Various artists have tried more elaborate schemes. It’s possible, for example, to draw or paint a picture so that you can tell what it is only if you look at its reflection in a mirror shaped like a cylinder or a cone. Other pictures must be reflected in shiny spheres, mirrored pyramids, or other reflecting shapes to reveal their true identity.
In the March American Journal of Physics, James L. Hunt and his colleagues at the University of Guelph in Ontario provide equations that describe the mathematical transformations underlying the most common anamorphic images found in art–the plane, cylindrical, and conical cases. The physicists even offer a service that transforms any submitted photograph into its anamorphic counterpart (see http://physics.uoguelph.ca/morph/main.html).
Artist Douglas D. Peden of Essex, N.Y., has explored another intriguing aspect of grid transformations to create visually arresting paintings, in which each gracefully distorted abstraction ripples its own, subtly musical tale.
“Transfiguration” by D. Peden. |
Peden started out in nuclear engineering, but he left the field during the 1960s to become an artist. In 1970, he moved to the Adirondack region of New York state. “I found the combination of the natural beauty and solitude supportive of my creative needs,” Peden says. “It also allowed me to pursue my own vision without the distraction and influence of the prevailing art fashions, styles, and market forces.”
Peden’s early paintings featured free-flowing amoebic forms radiating vibrant, contrasting colors. Later, he turned to abstract landscapes–trees, sky, water, land, and structures presented symbolically and rhythmically in great, horizontal swaths. His visual patterns, with their carefully manipulated thematic variations, reminded one of musical forms such as the classical sonata.
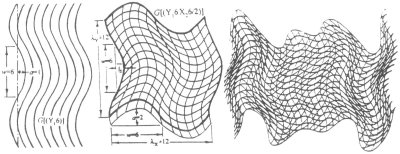
Peden then began to formalize his approach, developing a geometric language and framework that he could use to create his abstract narratives. Instead of working with a Cartesian grid represented by horizontal and vertical straight lines, Peden focused on coordinate systems based on wavy lines. He calls his scheme “wave space,” or “GridField,” geometry.
Specifying the wavelength and amplitude, he starts off with a set of wavy parallel lines oriented in the vertical direction. The corresponding set of lines in the horizontal direction is then chosen as a function of the vertical field. The combination produces what he calls a “gridfield” configuration. “If wave field amplitudes are reduced to zero, the gridfield becomes a Cartesian grid,” Peden notes. “In other words, the commonly used Cartesian grid system is one of many grid/gridfield configurations.”
Peden then weaves in another meandering wave field to produce additional distortions, making the final grid look like a strangely crumpled piece of fabric.
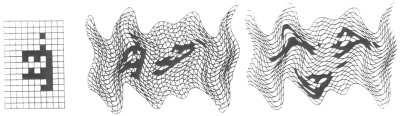
The choice of grid is up to the artist, as is the color of each of the grid’s cells. “The shapes, themes, rhythms, and spatial textures are defined and influenced by the geometric configuration of the chosen space,” Peden says.
A character drawn on a square grid can change shape drastically when transferred to different gridfields and to different positions within a given gridfield. |
“I enjoy the fact that my art includes and is inspired by such disciplines as music, literature, philosophy, mathematics, and physics,” Peden notes. “I feel the most profound art is that which encompasses all life–at least as much as one can experience within one’s limited capacity for knowledge, understanding, and expression.”
Peden’s work helps shed light on the apparent tension between artistic freedom and mathematical constraint. Like many artists, Peden has built a distinctive vision and style out of constraint–by exploring the seemingly unlimited, surprisingly rich possibilities offered by the set of rules that he developed (and freely chose) as the framework for his art.






