How two outsiders tackled the mystery of arithmetic progressions

Consider this sequence of numbers: 5, 7, 9. Can you spot the pattern? Here’s another with the same pattern: 15, 19, 23. One more: 232, 235, 238.  

“Three equally spaced things,” says Raghu Meka, a computer scientist at UCLA. “That’s probably the simplest pattern you can imagine.”  

Yet for almost a century, mathematicians in the field of combinatorics have been puzzling out how to know whether an endless list of numbers contains such a sequence, called an arithmetic progression. In other words, is there a way to be mathematically certain that a set contains a sequence of three or more evenly spaced numbers, even if you don’t know much about how the numbers in the set were selected or what the progression might be? 

Progress on the question has been slow, even plodding. But last year, Meka and Zander Kelley, a Ph.D. computer science student at the University of Illinois Urbana-Champaign, surprised mathematicians by making an exponential leap. The researchers are outsiders in combinatorics, which is concerned with counting configurations of numbers, points or other mathematical objects. And the duo didn’t set out to tackle the mystery of arithmetic progressions.  

Kelley and Meka were instead investigating abstract games in computer science. The pair sought a mathematical tool that might help them understand the best way to win a particular type of game over and over again. “I’m super-interested in a collection of techniques that fall under this umbrella called structure versus randomness,” Kelley says. Some of the earliest progress on arithmetic progressions relied on such techniques, which is what led Kelley and Meka to dive into the topic. 

The mystery of whether arithmetic progressions will show up is just one of many mathematical questions related to order versus disorder in sets of objects. Understanding order — and when and where patterns must emerge — is a recurring theme in many branches of math and computer science.  

Another example of order in objects says that any group of six people must contain either a group of at least three mutual acquaintances (all three know each other) or a group of at least three complete strangers (no one knows another). Research has shown that it doesn’t matter who they are, where they are from or how they were selected. There’s something powerful, maybe almost spooky, about the fact that we can say this — and make other similar claims about structure in sets — with mathematical certainty. 

Solving the mystery of arithmetic progressions might open doors to investigating more complex relationships among numbers in a set — gaps that change in more elaborate ways, for instance. “These are more sophisticated versions of the same theorems,” says Bryna Kra, a mathematician at Northwestern University in Evanston, Ill. “Typically, once you see arithmetic progressions … you see other patterns.”  

After publishing their work on arithmetic progressions, Kelley and Meka, with Shachar Lovett of the University of California, San Diego, imported techniques from their investigations of arithmetic progressions into a different context. The researchers solved a question in communication complexity, a subfield of theoretical computer science concerned with transmitting data efficiently between parties who have only partial information. 

What’s more, knowing that certain mathematical structures have to appear in certain situations can be useful in real-world communication networks and for image compression. 

Potential applications aside, researchers who study arithmetic progressions — or other facets of purely theoretical mathematics — are often motivated more by sheer curiosity than any practical payoff. The fact that questions about such simple patterns and when they appear remain largely unanswered is, for many, reason enough to pursue them. 

What are arithmetic progressions? 

Let’s take a moment to get our hands on some sets of numbers and the arithmetic progressions those sets contain, starting with the prime numbers, perennial favorites of math enthusiasts. A prime number is any whole number divisible only by itself and by 1; the first 10 primes are 2, 3, 5, 7, 11, 13, 17, 19, 23 and 29. Within those numbers, we can find a few arithmetic progressions. The numbers 3, 5 and 7 form a three-term arithmetic progression with a gap of two. But the numbers in a progression don’t have to follow each other immediately within the larger set: The numbers 5, 11, 17, 23 and 29 form a five-term arithmetic progression with a gap of six. 

Within a finite set of numbers, it’s straightforward to determine whether there are any arithmetic progressions. It might be tedious depending on the set, but it’s not mysterious. For infinite sets of numbers, though, the question gets interesting.  

The primes go on forever, and mathematicians have asked many — and answered some — questions about arithmetic progressions within them. Is there a longest possible arithmetic progression, a cap on the number of terms, in the primes? Or, can you find a progression of any finite length if you look long enough? In 2004, mathematicians proved that the latter is true. But questions including how far along the number line you have to look to find an arithmetic progression with a given number of terms or a given gap size remain active areas of research, for the primes and for other sets. 

The primes contain infinitely many arithmetic progressions, but some infinite sets contain none. Consider the powers of 10: 1, 10, 100, 1,000…. The gaps between consecutive terms get bigger fast — 9, 90, 900…. And none of them are the same. Playing around with the numbers a bit, you can convince yourself that no two powers of 10, whether consecutive or not, have the same gap as any other pair. 

With that context, we now approach a question at the heart of this research: Why do some sets have arithmetic progressions while others don’t? One big difference between the primes and powers of 10 is that there are a lot more primes than powers of 10. Sort of. Both sets are infinite, but if you pick any arbitrary number as a cutoff and look at how many primes or powers of 10 there are below that number, the primes win every time. There are four primes from 1 to 10, versus only two powers of 10. There are 25 primes from 1 to 100 and only three powers of 10. The primes don’t just win every time, they win by a lot, and the amount they win by keeps increasing. In this way, the primes are “denser” — in an intuitive and technical sense — than the powers of 10.  

A sparse enough set of numbers can have gaps arranged in ways that manage to avoid arithmetic progressions. Too dense, though, and the set can’t avoid having gaps that match up. In the 20th century, mathematicians settled on a way to measure that density. They are now looking for the density above which arithmetic progressions must appear. 

Density in infinite sets

The study of arithmetic progressions in sets of whole numbers began in earnest in 1936, when Hungarian mathematicians Paul Erdős and Pál Turán posited that any set of whole numbers that is dense enough must contain arithmetic progressions of any desired length. 

For finite sets, it’s easy to understand what density is. In the set of whole numbers between 1 and 10, the primes have a density of 4/10, or 0.4. But if we want to understand the density of the entire unending collection of prime numbers within the entire unending collection of the whole numbers, we need to find a way to make sense of infinity divided by infinity, or ∞/∞.  

Mathematicians use a concept called asymptotic density to wrangle with the density of an infinite set of whole numbers. The basic idea is to choose some number as a cutoff point, N, and see what happens as N increases. If the density tends toward some fixed number, that is the set’s asymptotic density.  

Let’s return to the powers of 10, whose density decreases across the number line. As you go out farther and farther, the proportion of whole numbers that are powers of 10 approaches zero — so the set has an asymptotic density of zero. Other sets have a positive asymptotic density, and some never settle down into an asymptotic density at all.  

What Erdős and Turán proposed is that any set of numbers with positive, rather than zero, asymptotic density must contain at least one arithmetic progression. For some sets, it’s obvious (the even numbers have an asymptotic density of 0.5 and definitely contain arithmetic progressions). But proving it for any arbitrary set of numbers turned out to be a challenge. 

It wasn’t until 1953 that German-British mathematician Klaus Roth proved the conjecture, opening the door to a more nuanced understanding of the role density plays in arithmetic progressions. He showed that any set with positive asymptotic density must contain at least one three-term arithmetic progression, or 3-AP. His argument relied on proving that dense enough pseudorandom sets — those that might not truly be chosen randomly but have the general properties of random sets — must contain arithmetic progressions. Then he developed a way to zoom in on parts of non-pseudorandom sets and show that, if the initial set is dense enough, these zoomed-in areas must be structured in ways that guarantee the presence of an arithmetic progression.  

In early 2021, Kelley and Meka were investigating a problem in complexity theory called parallel repetition of games. Don’t think Monopoly or chess; the “games” the researchers were thinking about won’t be making Hasbro money any time soon. “We have a tendency to call anything a game if it has turns,” says Kelley. In the typical games Kelley and Meka were looking at, the players have access to different information and have to work together to find an answer to a question. But they can’t communicate during the game, so they must decide on a strategy beforehand. Kelley and Meka sought to determine how to maximize the chances that the players win many games in a row. 

It’s not quite a hop, skip and a jump from parallel repetition of games to arithmetic progressions, but Kelley and Meka got there fairly quickly. “Maybe in a month we were at the 3-AP problem,” Meka says. Previous research on parallel repetition of games had used structure versus randomness arguments. Because Roth’s work on arithmetic progressions was the first to use such a technique, Kelley and Meka were interested in that work in its original habitat. 

“In theoretical computer science, people are looking outward to math for some tools that they could use, and unless you’re ready to get yourself into some serious trouble, usually you see if you can use the tools, and then if you can’t, you move on,” Kelley says. “You don’t try to go open them up and see what they’re like.” But he and Meka did just that, knowing that they might go down a deep rabbit hole and end up with nothing to show for their time and effort. They dug into Roth’s arguments — as well as more recent research on the same subject — to see if they could push the work further. And so they found themselves staring down arithmetic progressions. 

Reaching new limits 

Roth’s contribution was more powerful than just showing that any set with positive asymptotic density must contain a 3-AP. He also proved that some sets with asymptotic density of zero, if the density tends toward zero slowly enough as you go out along the number line, must also contain at least one 3-AP.  

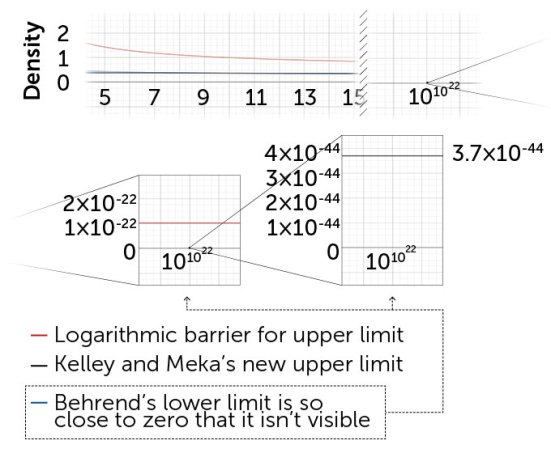
Think of the density as having to pass beneath a limbo bar. If a set gets sparse too slowly, it can’t make it under and it must contain an arithmetic progression. But a set that approaches a density of zero quickly enough ducks under. For that set, anything goes: It may or may not have such a progression. 

Roth’s initial proof found an upper limit to where the limbo bar must be. He showed that any set whose density approaches zero at a rate similar to or slower than the expression 1/log(log(N)) must contain at least one arithmetic progression. Log means to take the logarithm, and remember that N is the number chosen as the arbitrary cutoff in an infinite set. We’re considering what happens as N increases.  

Logarithms grow slowly, roughly akin to the number of digits a number has. The logarithm of 1 is zero, of 10 is 1, of 100 is 2, of 1,000 is 3, and so on. But taking the logarithms of those logarithms gives much more sluggish growth. To nudge log(log(N)) from zero to 1, we have to move N from 10 to 10 billion. Dividing 1 by this double log, as appears in Roth’s work, we get a density that just plods toward zero. 

Several years earlier, in 1946, mathematician Felix Behrend had investigated the lower limit of the limbo bar. He developed a recipe for cooking up sets without 3-APs, showing that any such set must be extremely sparse indeed. His limit was a density that goes to zero at approximately the same rate as 1/e^{(log(N))^½}. That expression might not look familiar, but there’s an exponential function in the denominator. The log and ½ power slow things down a bit, but the whole expression goes to zero much faster than the double log Roth later found. 

In the last few decades, researchers have been attempting to close the gap between Roth-style estimates of the sparsest sets that must contain a 3-AP and Behrend-style estimates of the densest sets that do not contain one. In 2020, mathematicians Thomas Bloom of the University of Oxford and Olof Sisask of Stockholm University broke what had come to be known as the logarithmic barrier for the Roth-style upper limit of the limbo bar, showing that any set with a density that goes to zero more slowly than 1/log(N) must contain at least one 3-AP. The work was seen as a breakthrough in the field, though the upper limit was still closer to the previous best-known upper limit than to Behrend’s lower limit.  

Kelley and Meka pushed the upper limit down dramatically. Their result was a rate that goes to zero at approximately the same rate as 1/e^{(log(N))^1/11}. That formula looks eerily similar to Behrend’s lower limit. For the first time ever, the upper and lower limits are within shooting distance of each other. Closing that gap would reveal the specific location of the limbo bar and thus give a clear answer to which sets must contain at least one 3-AP. 

What’s next? 

When Kelley and Meka started on the 3-AP problem, they thought they would probably just poke around to identify the barriers to moving the upper limit down. A year later, the two were writing a paper about their breakthrough. “I think one thing that kept us going was it never felt like we were completely hitting a wall,” Meka says. “It always felt like we were either learning something useful, or we were actually making progress.”  

Meka describes their overall approach, based on Roth’s early techniques, as exploiting a “wishful dichotomy” between randomness and structure. They developed a definition of pseudorandomness for their work and showed that for this definition, any dense enough pseudorandom set must contain at least one arithmetic progression. 

After handling the pseudorandom case, the team considered more structured sets of numbers and showed that those sets too had to exhibit the desired patterns. Finally, Kelley and Meka expanded from these types of sets to all large enough sets of numbers, proving that those sets must have the properties of either the pseudo­random or the structured sets.  

“Three equally spaced things. That’s probably the simplest pattern you can imagine.”

Raghu Meka

The most remarkable thing about Kelley and Meka’s work is that they were able to make such dramatic progress without developing a new approach to arithmetic progressions. Though they brought new insights and established new connections to previous work, they did not create new machinery.  

“It just seemed completely intractable to push those techniques through,” Sisask says, “until this paper by Kelley and Meka landed in my inbox.” He and Bloom, who had previously broken the logarithmic barrier, “spent a while digesting the paper and talking about it until we understood it in our own language,” he says.  

Mathematicians and computer scientists tend to use some different notation and terminology, but Sisask, Bloom and other experts in the field quickly recognized the work as solid. After digesting the arguments, Sisask and Bloom wrote an explanation of the work, with some subtle technical improvements, geared toward other researchers in combinatorics. Several months later, the team coaxed the upper limit down a tiny bit more, getting a new bound of 1/e^{(log(N))^1/9}. 

Combinatorics researchers are still trying to figure out how low they can go. Will they be able to push the upper limit all the way down to the best known lower limit, or will there always be a little gap where our knowledge is incomplete? Kelley and Meka are using the tools they honed on arithmetic progressions to continue work on problems in complexity theory and other areas of theoretical computer science. 

When I asked Meka how two computer scientists made such a big advance on a mathematics problem that had stumped combinatorics experts for years, he said he isn’t sure. He thinks maybe their edge came from being fresh to the challenge.  

“The problem has been around for a long time and progress seemed pretty stuck,” he says. In fact, after he and Kelley were well on their way to publishing, Kelley says he ran across a blog post from 2011 that outlined exactly why mathematicians were pessimistic about the very approach that the two had eventually used.  

“People thought that these techniques couldn’t push beyond existing barriers,” Meka says, “but maybe we didn’t know that the barriers existed.”