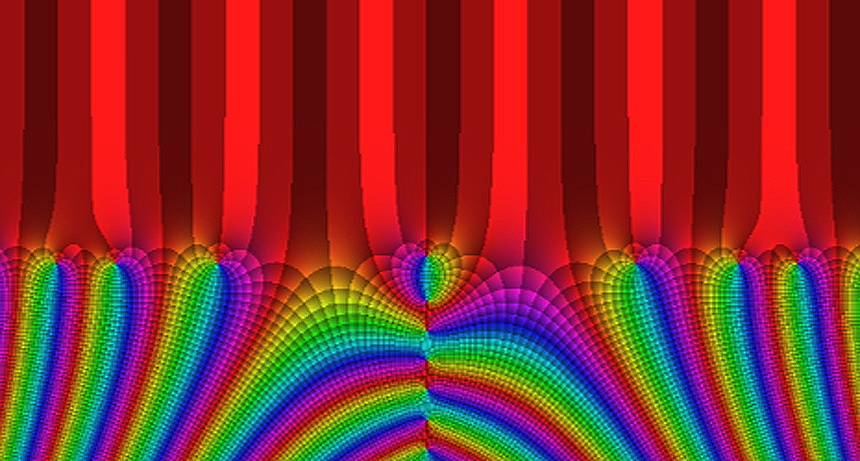
LINED UP The Riemann zeta function has an infinite number of points where the function’s value is zero, located at the whirls of color in this plot. The Riemann hypothesis predicts that certain zeros lie along a single line, which is horizontal in this image, where the colorful bands meet the red.
Empetrisor/Wikimedia Commons (CC BY-SA 4.0)
A famed mathematical enigma is once again in the spotlight.
The Riemann hypothesis, posited in 1859 by German mathematician Bernhard Riemann, is one of the biggest unsolved puzzles in mathematics. The hypothesis, which could unlock the mysteries of prime numbers, has never been proved. But mathematicians are buzzing about a new attempt.
Esteemed mathematician Michael Atiyah took a crack at proving the hypothesis in a lecture at the Heidelberg Laureate Forum in Germany on September 24. Despite the stature of Atiyah — who has won the two most prestigious honors in mathematics, the Fields Medal and the Abel Prize — many researchers have expressed skepticism about the proof. So the Riemann hypothesis remains up for grabs.
Let’s break down what the Riemann hypothesis is, and what a confirmed proof — if one is ever found — would mean for mathematics.
What is the Riemann hypothesis?
The Riemann hypothesis is a statement about a mathematical curiosity known as the Riemann zeta function. That function is closely entwined with prime numbers — whole numbers that are evenly divisible only by 1 and themselves. Prime numbers are mysterious: They are scattered in an inscrutable pattern across the number line, making it difficult to predict where each prime number will fall (SN Online: 4/2/08).
But if the Riemann zeta function meets a certain condition, Riemann realized, it would reveal secrets of the prime numbers, such as how many primes exist below a given number. That required condition is the Riemann hypothesis. It conjectures that certain zeros of the function — the points where the function’s value equals zero — all lie along a particular line when plotted (SN: 9/27/08, p. 14). If the hypothesis is confirmed, it could help expose a method to the primes’ madness.
Why is it so important?
Prime numbers are mathematical VIPs: Like atoms of the periodic table, they are the building blocks for larger numbers. Primes matter for practical purposes, too, as they are important for securing encrypted transmissions sent over the internet. And importantly, a multitude of mathematical papers take the Riemann hypothesis as a given. If this foundational assumption were proved correct, “many results that are believed to be true will be known to be true,” says mathematician Ken Ono of Emory University in Atlanta. “It’s a kind of mathematical oracle.”
Haven’t people tried to prove this before?
Yep. It’s difficult to count the number of attempts, but probably hundreds of researchers have tried their hands at a proof. So far none of the proofs have stood up to scrutiny. The problem is so stubborn that it now has a bounty on its head: The Clay Mathematics Institute has offered up $1 million to anyone who can prove the Riemann hypothesis.
Why is it so difficult to prove?
The Riemann zeta function is a difficult beast to work with. Even defining it is a challenge, Ono says. Furthermore, the function has an infinite number of zeros. If any one of those zeros is not on its expected line, the Riemann hypothesis is wrong. And since there are infinite zeros, manually checking each one won’t work. Instead, a proof must show without a doubt that no zero can be an outlier. For difficult mathematical quandaries like the Riemann hypothesis, the bar for acceptance of a proof is extremely high. Verification of such a proof typically requires months or even years of double-checking by other mathematicians before either everyone is convinced, or the proof is deemed flawed.
What will it take to prove the Riemann hypothesis?
Various mathematicians have made some amount of headway toward a proof. Ono likens it to attempting to climb Mount Everest and making it to base camp. While some clever mathematician may eventually be able to finish that climb, Ono says, “there is this belief that the ultimate proof … if one ever is made, will require a different level of mathematics.”






