Creeping Up on Riemann

Prime numbers are maddeningly capricious. They clump together like buddies on some regions of the number line, but in other areas, nary a prime can be found. So number theorists can't even roughly predict where the next prime will occur. The distribution of primes is the great motivating question of number theory.

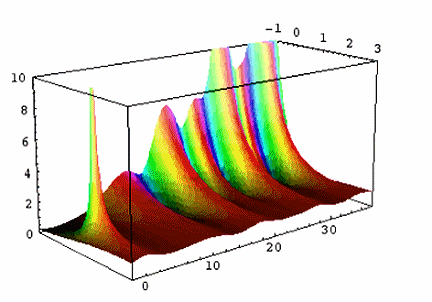
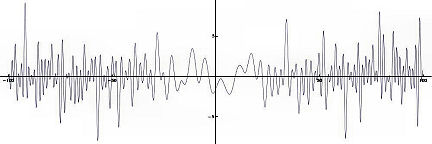
Prime numbers are like the atoms of mathematics: the simple, indivisible building blocks upon which all the other numbers are built. By definition, a prime number isn't divisible by any number except itself and 1; so, for example, 5 is prime but 4 is not, since 4 = 2 × 2. But while the atoms of chemistry are neatly arranged in a periodic table, the search for a pattern in primes keeps number theorists pondering as they lie in bed at night.

Vexingly, the answer to their questions lies encoded within a single function—one that happens to be enormously difficult to fully understand. The "Riemann zeta function" contains within it the key to the distribution of the prime numbers. But mathematicians have been working on uncovering the function's mysteries since 1859, when Bernhard Riemann formulated a much-celebrated hypothesis about it, and so far, they haven't cracked it. With the recent solutions to Fermat's Last Theorem and the Poincaré conjecture, the Riemann hypothesis could now be considered the biggest puzzle in mathematics—and the Clay Mathematics Institute in Cambridge, Mass., will award the person who solves it a million dollars.

Two mathematicians, Ce Bian and Andrew Booker of the University of Bristol in England, now have the first glimpse of an elusive mathematical object that may one day help crack the problem. They have found the first example of a third-degree transcendental L-function.

"There is hardly a problem in number theory that doesn't seem to be connected to L-functions," says Michael Rubinstein of the University of Waterloo in Ontario, Canada. But these functions, though incredibly numerous, have also been incredibly hard to find. "It's like what biologists must feel when finding a new species they'd only seen tracks from before," he says. "You know they're out there and you're trying to find them. Now we've got one."

Mathematicians attack really hard problems like the Riemann hypothesis with a strategy that might initially seem odd: they try to prove a claim that is even bigger and bolder than the original one. By embedding the problem in a larger context, they can build bigger tools to attack it.

To see why that might be useful, imagine that a mosquito is pestering you. If you can't manage to swat it, you might instead try a bug bomb, killing every insect in the room—and being sure to get that darn mosquito in the process. Thus killing all the bugs might be easier than simply killing the one wily mosquito. This technique of generalization is the same one that brought down both Fermat's Last Theorem and the Poincaré conjecture.

In the case of the Riemann hypothesis, mathematicians are considering the whole family of L-functions, of which the Riemann zeta function is just one. They've generalized the Riemann hypothesis to all the L-functions, and they want to use this bigger, badder version to kill the "mosquito" of the original function along with all the others.

Unfortunately, mathematicians haven't had a single example of an L-function that is reasonably complex to work with. The simplest examples, like the Riemann zeta function, have been known for a long time, and somewhat more complex versions were featured prominently in Andrew Wiles' proof of Fermat's Last Theorem. But the functions get vastly more sophisticated than that, and an understanding of these more complex versions will likely be necessary to prove the Riemann hypothesis.

Until just over a decade ago, mathematicians hadn't even proven that these very complex functions existed. And when Stephen D. Miller of Rutgers University in New Jersey did prove it, he did so indirectly, without providing a single example. So, many number theorists have put a great deal of effort into understanding a type of function they had never even seen. Now, with the aid of 10,000 hours of computing time on a PC, Bian and Booker have finally tracked one of these functions down.

"It's an amazing computation," says Don Blasius of the University of California, Los Angeles. "It solves a computationally extremely challenging problem that would have been literally undoable until now."

Finding the function required a combination of computational cleverness and theoretical advances. Bian and Booker couldn't find it with absolute exactness because that would involve finding infinitely many irrational numbers that occur in the function. But the researchers deduced the first few hundred of these numbers, to within about 6 decimal places.

Oddly, Booker points out, even though mathematicians had never seen one of these functions, they knew a lot about what they had to be like. The researchers could check their result by making sure their function had all the properties it was expected to have. One of the checks on the computation involved checking the generalized Riemann hypothesis for this particular case. "We're totally confident in our result," Booker says.

Mathematicians will be thrilled if they do someday succeed in proving the Riemann hypothesis, but odds are that they have a long way to go. Booker freely says that his result is just one small step along the way. "Is this thing going to solve the Riemann hypothesis? Well, no," he says. But it may contribute to a solution eventually, and in the meantime, it certainly has some mathematicians excited.

If you would like to comment on this article, please see the blog version.