The notion of a simple equation that you can use to generate a wide variety of geometric shapes is an immensely appealing one. Johan Gielis of Antwerp, Belgium, proposes one such formula in the March American Journal of Botany.

![]()
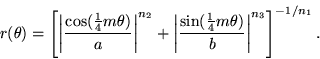

“Many geometrical forms, both in nature and culture, can be interpreted as modified circles,” Gielis states. These shapes, he contends, are useful for modeling natural structures and providing insight into why certain forms grow as they do.
Gielis starts with the equation for a set of shapes called superellipses:
By selecting appropriate values of a, b, and n, you can generate various circles, ellipses, rectangles, and other symmetric forms. For instance, when a = b and n = 2, the formula produces a circle.
The same formula can be expressed in polar coordinates, where the locations of points are expressed in terms of angle, q, and distance, r, from the origin rather than x and y coordinates. This means making the following replacement in the formula: x = r cos q and y = r sin q.
To allow additional rotational symmetries, Gielis also introduces the angle parameter m/4. The result, which he dubs the superformula, is a generalization of the superellipse formula to encompass many more shapes:
When n1 = n2 = n3 = 2 and m = 4, the formula generates an ellipse. A circle is the special case when a = b.
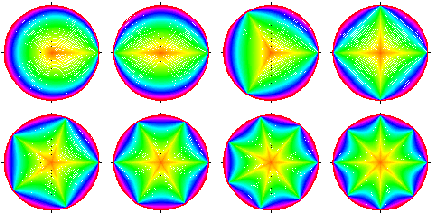
In experimenting with his superformula, Gielis generated a variety of shapes reminiscent of natural forms. The following set of diagrams shows a number of these shapes.
From left to right: Nuphar luteum petiole (a = b = 1, m = 3, n1 = 4.5, n2 = n3 = 10), Scrophularia nodosa stem (a = b = 1, m = 4, n1 = 12, n2 = n3 = 15), Equisetum stem (a = b = 1, m = 7, n1 = 10, n2 = n3 = 6), raspberry (a = b = 1, m = 5, n1 = n2 = n3 = 4), and starfish (a = b = 10, m = 5, n1 = 2, n2 = n1 = 7). |
The superformula “allows us to understand the mathematical simplicity and beauty of many natural forms differing only in parameter values,” Gielis claims. It permits “a great reduction of complexity in shapes and provides new insights into symmetry.”
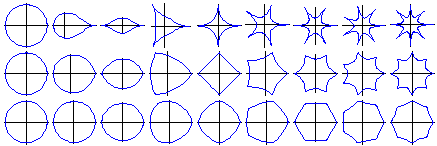
Varying parameters in Gielis’ superformula produces a range of different shapes. |
“Given the extraordinary correspondence to natural shapes,” Gielis continues, “we can postulate that [the superformula unveils] a very basic geometry of nature. . . . [It] inherently allows for small modifications of parameters . . . and can become a powerful tool in the study of nature.”
It isn’t at all clear whether the equation formulated by Gielis will have any impact in biological circles on questions concerning the symmetry and shape of natural forms. Nonetheless, his formula provides new opportunities for entertaining and colorful graphic explorations.
Families of curves generated by Gielis’ superformula when a = b = 1, m varies, and n = n1 = n2 = n3, going from n = 1 (top left) to n = 8 (bottom right). |






