In 1840, the Danish artist Christian Albrecht Jensen (1792–1870) was commissioned to paint a portrait of the renowned mathematician Carl Friedrich Gauss (1777–1855). This portrait, showing Gauss at the venerable age of 63, went on display at the Pulkowa Observatory in St. Petersburg, Russia, where it remains to this day.
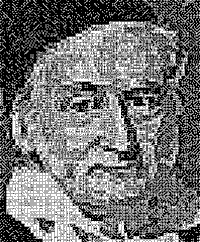

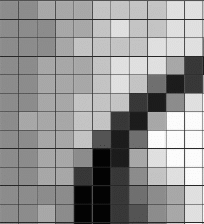



![]()

That painting of Gauss has been copied many times over the years, with variants of the portrait even appearing on bank notes and postage stamps.
A portrait of Carl Friedrich Gauss (left) constructed from 48 complete sets of dominoes (detail, right).Courtesy of Robert Bosch. |
|
One recent rendition of the Gauss portrait was constructed entirely from 48 complete sets of double-nine dominoes. The work of mathematician Robert Bosch of Oberlin College, this remarkable creation and others like it represent the successful application of a novel algorithm for approximating target images as arrays of dominoes.
To create a domino portrait, Bosch starts with an image—a picture of Gauss, Abraham Lincoln, Marilyn Monroe, John Lennon, or some other figure—and a certain number of complete sets of dominoes. His goal is to position the dominoes in such a way that, when seen from a distance, the assemblage looks like the target image.
What makes this task especially challenging is the self-imposed requirement of using complete sets. Hence, when Bosch works with 48 sets, he must use precisely 48 blank dominoes, 48 dominoes that have a blank square and a square with one dot, and so on. To make this work requires delicate compromises on the placement of constituent dominoes.
To find optimal positions for the dominoes, Bosch applies a mathematical technique known as integer programming. Long used in operations research, integer programming has aided schedule construction, route selection, and a variety of other large-scale planning tasks.
A portion of a digital image (top left) is divided into squares (top right) with grayscale values between 0 and 9 (bottom left). Bosch’s computer program then works out the arrangement of dominoes (bottom right) that gives the best possible match with the image’s grayscale values. Courtesy of Robert Bosch. |
|
Bosch’s computer program starts by dividing the target image into an array of squares. Some squares are completely white, others are completely black, and the rest are various shades of gray. White squares are assigned the value 9, black squares have the value 0, and gray squares are given intermediate values.
A domino is made up of two squares. A complete set consists of 55 dominoes—10 that are doubles and 45 that are not doubles. Each double has two possible orientations (horizontal or vertical), and each nondouble has four possible orientations. Clearly, double-blank dominoes would most likely go where the grayscale value is 0, and double-nine dominoes would most likely go where the grayscale value is 9.
Using integer programming, Bosch’s software determines the optimal placement and orientation of each of the available dominoes. In effect, it selects the arrangement that most closely matches the numbers that describe the original image. Choosing a larger number of sets of dominoes enables the rendering of a more accurate approximation of the original image.
A classroom project involving first- and second-graders produced this domino portrait of Martin Luther King Jr. Courtesy of Robert Bosch. |
Bosch has created more than 100 domino portraits. Some examples can be seen at http://www.dominoartwork.com/.






