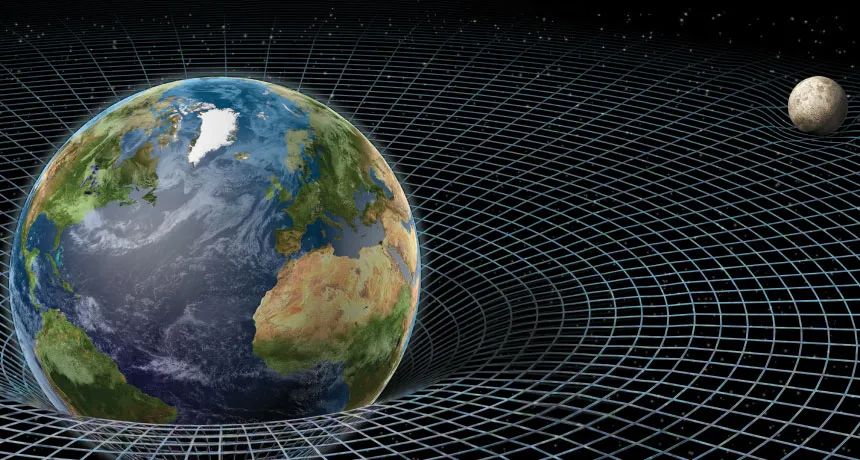
GETTING A GRIP ON GRAVITY Einstein's general theory of relativity explains gravity as a distortion of space (or more precisely, spacetime) caused by the presence of matter or energy. A massive object generates a gravitational field by warping the geometry of the surrounding spacetime.
Nicolle Rager Fuller
Albert Einstein opened humankind’s eyes to the universe.
Before Einstein, space seemed featureless and changeless, as Isaac Newton had defined it two centuries earlier. And time, Newton declared, flowed at its own pace, oblivious to the clocks that measured it. But Einstein looked at space and time and saw a single dynamic stage — spacetime — on which matter and energy strutted, generating sound and fury, signifying gravity.
Newton’s law of gravity had united the earthly physics of falling apples with the cosmic dances of planets and stars. But he couldn’t explain how, and he famously refused to try. It took an Einstein to figure out gravity’s true modus operandi. Gravity, Einstein showed, did not just make what goes up always come down. Gravity made the universe go ’round.
Gravity’s secrets succumbed to Einstein’s general theory of relativity, unveiled in a series of papers submitted a century ago this November to the Prussian Academy in Berlin. A decade earlier, his special theory of relativity had merged matter with energy while implying the unity of space and time (soon to be christened as spacetime). After years of struggle, Einstein succeeded in showing that matter and spacetime mutually interact to mimic Newton’s naïve idea that masses attract each other. Gravity, said Einstein, actually moved matter along the curving pathways embodied in spacetime — paths imprinted by mass and energy themselves. As expressed decades later by the physicist John Archibald Wheeler, mass grips spacetime, telling it how to curve, and spacetime grips mass, telling it how to move.
Einstein’s theory explained a famous observation that Newtonian gravity could not: a subtlety in the orbit of the planet Mercury. And his equations implied further slight deviations from Newtonian calculations. Over the last century, general relativity’s predictions have been repeatedly verified by modern precision measurements. To physicists today, general relativity and gravity are essentially synonyms.
But general relativity is about more than just understanding gravity. It’s about explaining the totality of existence. General relativity inspired a new vision of the entire fabric of the cosmos. From general relativity flowed the realization that the universe is expanding, that it contains spacetime bottomless pits called black holes, that it is traversed by ripples in space triggered by cataclysmic collisions.
“The implications for the further reaches of the universe were more surprising than even Einstein ever realized,” physicist Stephen Hawking has written.
General relativity explains how the universe can obey physical laws that apply to any form of motion. It’s at the heart of identifying and investigating crucial questions about space and time, existence and reality. And its implications are not limited to esoteric concerns on cosmic scales — it has its down-to-Earth impacts as well. Without general relativity, for instance, GPS devices would be worthless. Satellite signals designed to keep your car on the right road would be off by miles if not corrected for the effects predicted by Einstein’s math.
Gravitation revolution
On his road to general relativity, Einstein himself took many wrong turns. From 1907 to 1914 he struggled with what the physicist Abraham Pais called “one of the hardest problems of the century” — explaining gravity in a way that permits the laws of nature to be the same for all observers, no matter how they are moving. Einstein had to learn new math and jettison common prejudices, such as the universal belief that Euclidean geometry described reality accurately. He struggled with distractions, both in his personal life and in physics problems posed by quantum theory. And he found that nature stubbornly refused to cooperate. By 1914 he had essentially given up, believing that a partially successful attempt — a sort of general relativity lite — was the best that nature would allow.
But then somehow Einstein’s brain rebooted. His theory began to solidify, and he swiftly composed four papers, one a week, during November 1915. By the last paper he had finally found the decisive equation that launched his gravitation revolution.
Four years later, general relativity made Einstein himself a celebrity. If gravity curves space, he had realized early on, a light beam passing near a massive object (say, the sun) would be deflected from its course. That deflection would shift the apparent position of the source of the light (say, a distant star). During a solar eclipse, such a shift could be photographed and measured. Such measurements, made during eclipse expeditions in 1919, confirmed Einstein’s calculation. Even without Twitter to spread the word, Einstein’s triumph sparked a media sensation.
“Lights all askew in the heavens, men of science more or less agog,” proclaimed one of the most famous newspaper headlines in science history, in the Nov. 10 New York Times. And from the Times of London on November 7: “Revolution in Science, New Theory of the Universe, Newtonian Ideas Overthrown.”
Einstein became a legend, his name forevermore synonymous with genius.
As it turned out, some bending of light would have been expected even with Newtonian gravity, as Johann von Soldner had calculated (unknown to Einstein) more than a century earlier. But Einstein predicted precisely twice as much bending as von Soldner had. And although the earliest measurements were crude, they were much closer to Einstein’s predictions than Newton’s. In subsequent eclipses, Einstein’s calculation has been repeatedly confirmed. Gravity deflects light just as general relativity requires.
General relativity’s light-bending effect proved valuable for much more than affirming Einstein’s theory. By bending light, masses act like a lens; such “gravitational lensing” alters the apparent position of a distant object, creating multiple images of it, or (if the images overlap) appearing to brighten it. Such effects can be used to probe matter’s distribution in space or detect the presence of unseen masses.
“Since the discovery of the first gravitational lens, the phenomenon has been exploited to map the distribution of mass around galaxies and clusters, and to search for dark matter, dark energy, compact objects, and extrasolar planets,” physicist Clifford Will notes in a recent paper.
Gravitational lensing was first observed in 1979, but Einstein had suspected its possibility in 1912, even before his theory had been completed. Only in 1936 did he publish a paper about it, Will notes, “primarily, it seems, to get a Czech electrical engineer named Rudi Mandl to stop pestering him about it.” Will, of the University of Florida in Gainesville, does not mention that Mandl had first approached Science News Letter (Science News’ predecessor) with the gravitational lens idea; the magazine paid his expenses to visit Einstein, who then agreed to do the calculation that Mandl had suggested (SNL: 12/19/36, p. 388). Einstein’s paper, published in Science, suggested that the effect would never be noticed. But modern astronomical explorations proved the contrary.
Einstein was also ambivalent about other consequences of general relativity. In 1916, for instance, he raised the possibility of gravitational radiation — waves rippling through spacetime after a massive body abruptly changes its motion, as when colliding with another mass. Such waves should exist, Einstein reasoned, because general relativity required gravity’s influence to propagate at the speed of light (whereas Newton’s gravity transmitted itself instantaneously). But later Einstein changed his mind. In 1936, he and Nathan Rosen submitted a paper arguing that such waves did not exist after all. But their paper contained a mistake. Today, gravitational waves’ reality has been established convincingly by indirect methods, and experiments to detect them directly are under way (see “Magnifying the Cosmos”).
Astronomers have already detected another offspring of general relativity, black holes, throughout the cosmos. But Einstein didn’t believe they would exist, either.
Black holes’ existence had been foreshadowed only weeks after Einstein presented his general relativity papers to the Prussian Academy. Karl Schwarzschild, a German astronomer serving in World War I on the Russian front, worked out solutions to Einstein’s complicated equations for the spacetime geometry around a massive sphere. It was the first mathematical step toward describing black holes in space. But Schwarzschild didn’t pursue the topic; he died a few months later from a skin disease. Not until the late 1960s did black holes emerge as general relativity’s most prominent advertisement, stimulating both science and the popular imagination. They became the most glamorous product of a theory conceived by science’s best imaginer.
Falling freely
Einstein’s imagination gave birth to general relativity’s core idea as he gazed out his office window while he was supposed to be evaluating patents. “All of a sudden I was struck by a thought,” Einstein later said. “If a person falls freely, he will certainly not feel his own weight.”
It was 1907, two years after his special theory of relativity had rewritten textbook notions about time and motion.
Special relativity showed that the laws of nature don’t depend on how you are moving, as long as it’s uniform motion — constant speed in a straight line. But in real life, objects and people move in all sorts of nonuniform ways. (Let the air out of a balloon, for instance.) Even some “simple” motions, like the rotation of a sphere or orbit of a planet, are nonuniform, as they constantly change direction and are therefore accelerating. Einstein wanted to extend relativity to all forms of accelerated motions. But he didn’t know how.
Then his happy thought in the patent office raised hope. A person falling freely accelerates toward the ground because of gravity but feels no force (until impact). Therefore, Einstein realized, gravity and acceleration are two sides of a coin. The upward thrust of an accelerating rocket ship pins the occupants to the floor just as the gravitational pull of the Earth keeps your feet on the ground. This acceleration-gravity equivalence explained a curious Newtonian coincidence: A body’s mass (its inertial resistance to changes in motion) is equal to its weight (or gravitational mass), its response to gravity. Einstein built special relativity on the principle that light’s velocity was constant; he suspected that general relativity could be built on the principle that inertial and gravitational mass are equivalent. If he succeeded, it would mean that nature’s laws could be the same for all forms of motion.
At first progress was slow. Then a key clue emerged in 1908, when the mathematician Hermann Minkowski showed how special relativity required the merger of space with time (SN: 9/13/08, p. 26). In special relativity, measures of space or time differ for different observers. But Minkowski showed that space and time combined — spacetime — yielded a mathematical description of events that all observers could agree on. Any event’s location could be specified by a set of space and time coordinates.
Establishing such coordinates requires a frame of reference, or origin point. Different observers will choose different origins. So if nature’s laws are the same for everybody, then any one person’s set of coordinates should in some sense be equivalent to anybody else’s. Einstein’s quest, then, became an effort to find the formula for transforming any one coordinate system into any other, while maintaining the equivalence between gravity and acceleration.
By 1912, Einstein realized that his goal would require abandoning Euclidean geometry. Real space, he realized, could not conform to the idealized lines and angles of the textbooks. Gravity distorted the coordinates, just as a grid of straight lines on a rubber sheet would curve if you placed a heavy cannonball on it.
But Einstein did not possess the mathematical skills to cope with non-Euclidean geometry. Fortunately, his college friend Marcel Grossmann, an accomplished mathematician, was eager to help. Familiar with 19th century–mathematician Bernhard Riemann’s work on the math for describing curved surfaces, Grossmann helped Einstein produce the outline (Entwurf in German) of a new gravity theory. It had one drawback, though — it worked for some coordinate systems, but not all possible systems. Einstein was dismayed, writing to the physicist Hendrik Lorentz in August 1913 that “there are still such major snags in the thing that my confidence in the admissibility of the theory is still shaky.” If acceleration is equivalent to a gravitational field, Einstein noted, every kind of acceleration should be describable by the equations for gravity. If not, “the theory refutes its own starting point; then it has no foundation whatsoever.”
Two days later, Einstein seemed much happier, writing to Lorentz that the Entwurf theory’s deficiency had been solved. In November, Einstein described that solution in a letter to physicist Paul Ehrenfest, asserting that equations describing all accelerations simply couldn’t exist; some coordinate systems get special status in order to preserve the law of energy-momentum conservation. That made his original goal impossible. But Einstein seemed satisfied that he had done the best that nature would permit.
“Can there be anything more beautiful than this, that the necessary specialization follows from the conservation laws?” Einstein asked Ehrenfest. It turned out that there actually was something more beautiful. But to find it, Einstein had to move to Berlin.
Breakthrough in Berlin
Einstein’s life until then had been peripatetic. Born in Ulm, Germany, in 1879, he moved when an infant to Munich and then as a teenager to Milan, Italy, having dropped out of high school. He went back to school in Switzerland, eventually graduating from college in Zurich. Failing to find an academic job, he joined the Swiss patent office in 1902, and the next year married Mileva Marić.
During his years at the patent office, Einstein produced an explosive output of papers poking holes in traditional physics, including reports on his special theory of relativity and Nobel Prize–winning work on quantum physics. Eventually those papers led to sufficient recognition in the physics world to get a faculty appointment in Prague. But at the first chance he returned to Zurich, where Grossmann now taught math. There Einstein and Grossmann developed the Entwurf theory. And then Berlin, the pinnacle of German (and world) physics, called. Prominent physicists at the university there made Einstein an offer he couldn’t refuse: no teaching responsibilities. As he wrote to Lorentz: “I could not resist the temptation to accept a position in which I am relieved of all responsibilities so that I can give myself over completely to rumination.”
Story continues below box
Throughout all these moves, Einstein’s personal life deteriorated. Growing apart from Mileva, he pursued a relationship with his cousin Elsa. And Mileva did not relish the idea of life in Berlin. In July 1914 she took their two sons back to Zurich, and Einstein was left in Berlin free to ruminate about general relativity to his heart’s content. During the following year his freedom nourished a fertile few months in which he saw a new path to success. In mid-1915 he saw that there was a way to make relativity truly general. Rather than imposing energy-momentum conservation on the equations, he worked on devising equations that would impose the conservation law on the universe.
Einstein now applied the full force of all the mathematical wizardry he had mastered in the preceding years, adopting embellishments of Riemann’s math called tensors. By November 1915, Einstein sensed victory. On November 4, he submitted a paper on general relativity to the Prussian Academy, following up with an addendum November 11. The next week, he presented yet another new paper, this time in a lecture to the academy, showing how general relativity’s spacetime curvature solved the outstanding gravitational problem in all of physics, the anomaly in the orbit of Mercury. During the following week, he finally found the correct form for the equations describing the gravitational field, presenting his result on November 25. Einstein’s quest was completed. General relativity worked.
Universal implications
Einstein quickly realized (or had known all along) that his new theory of gravity was really a theory of the cosmos. In 1917, he wrote a famous paper applying general relativity to the universe as a whole. Today that paper stands as the foundation for modern cosmology. But at the time, Einstein was troubled — his equations implied an unstable universe, either growing or collapsing. In those days, the universe was supposed to be eternal, everlasting and changeless. So Einstein altered his equation, adding a factor called the cosmological constant, representing a constant energy density in space that kept the universe static.
Others didn’t buy it. Alexander Friedmann, a Russian meteorologist-mathematician, developed a description of an expanding or contracting universe from Einstein’s original equations. Einstein first thought Friedmann to be in error, but then relented, although still viewing the “expanding universe” as of mathematical interest only. But a few years later, when Edwin Hubble’s analysis of light from distant galaxies confirmed the universe’s expansion, Einstein gave in. Despite his own reluctance to accept it, Einstein’s general relativity math did in fact imply what Wheeler later called the “most dramatic prediction that science has ever made” — the expansion of the universe.
Today, Einstein’s cosmological constant has been revived. Rather than preventing the universe from collapse, the vacuum energy it describes can explain why the universe now expands at an accelerating pace. General relativity, cosmological constant and all, today forms the core science for analyzing the history of the universe and forecasting its future.
But apart from its use in cosmology, general relativity was not widely applied to scientific problems in its first four decades. For the most part, general relativity languished in departments of mathematics, rarely studied in physics.
“General relativity was essentially a dead subject for a long time,” says the prominent relativity theorist Wolfgang Rindler of the University of Texas at Dallas. “People considered it a dormant science.”
Only after Einstein died in 1955 did general relativity come to life. About that time Wheeler, at Princeton University, began a program to explore its implications and train students to pursue them. By the early 1960s, new astronomical phenomena demanded explanations that Newtonian physics could not provide, and general relativity was poised for its renaissance. In the decades that followed, general relativity proved crucial for describing all sorts of celestial phenomena. At the same time, physicists devised ever more precise tests of its predictions, and Einstein passed them all. As Will has noted, “It is remarkable that this theory, born 100 years ago out of almost pure thought, has managed to survive every test.”
Even harder than finding the equations for general relativity is explaining how, out of almost pure thought, Einstein did it. Science historian Gerald Holton once remarked, while describing Einstein in the context of defining scientific genius, that “there is a mutual mapping of the mind and lifestyle of this scientist, and of the laws of nature.” Einstein himself ascribed his success to discovering the deep relationship between mathematics and the physical world.
In creating general relativity, Einstein’s path was forked; he had to envision physical processes governing matter, space and time, while at the same time formulating abstract mathematical expressions corresponding to that reality. As a student, Einstein testified, he neglected mathematics. His intuition was not strong enough to guide him to the most profound of math’s many subfields. But in the physical realm of natural phenomena, “I soon learned to scent out that which was able to lead to fundamentals and to turn aside from … the multitude of things which clutter up the mind and divert it from the essential.” At first he didn’t realize that “a more profound knowledge of the basic principles of physics is tied up with the most intricate mathematical methods.” He learned that from his pursuit of general relativity.
In the end, Einstein’s mind produced a mathematical theory so rich that it entailed unsuspected cosmic novelties. Fantastic physical phenomena were first discovered not through the lenses of telescopes, but within the squiggles Einstein had scratched out on paper to make the world make sense — to him. And now physical nature makes sense to modern science only because of Einstein’s insights.
“Einstein’s ideas,” his friend the physicist Max Born wrote over half a century ago, “have given the physical sciences the impetus which has liberated them from outdated philosophical doctrine, and made them one of the decisive factors in the modern world of man.”
This article appears in the October 17, 2015, Science News with the headline, “Getting a grip on gravity: Einstein’s genius reconstructed science’s perception of the cosmos.”
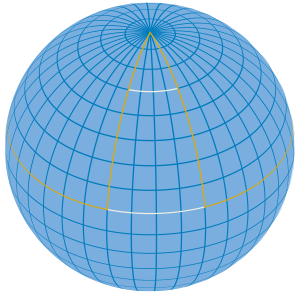 The curvature of spacetime lies at the heart of general relativity. The theory predicts that anything moving through a gravitational field undisturbed by other forces will follow a curved path called a geodesic. Geodesics on two-dimensional curved surfaces, like the Earth’s, illustrate how curvature creates gravity. From any point on the equator, for instance, the shortest path to the North Pole follows a curve — the geodesic corresponding to a meridian. If two people start out on such a trek, starting some distance apart, they pursue different curved meridians to the pole but grow closer together as they travel northward. It would appear that the curvature was pulling them towards each other — just as Newton’s gravity described.
The curvature of spacetime lies at the heart of general relativity. The theory predicts that anything moving through a gravitational field undisturbed by other forces will follow a curved path called a geodesic. Geodesics on two-dimensional curved surfaces, like the Earth’s, illustrate how curvature creates gravity. From any point on the equator, for instance, the shortest path to the North Pole follows a curve — the geodesic corresponding to a meridian. If two people start out on such a trek, starting some distance apart, they pursue different curved meridians to the pole but grow closer together as they travel northward. It would appear that the curvature was pulling them towards each other — just as Newton’s gravity described. In the middle of the 19th century, astronomers discovered that the orbit of Mercury doesn’t quite conform to the path predicted by Newtonian gravity. On each trip around the sun, Mercury’s closest approach, or perihelion, shifts forward by a slight amount, less than 2 degrees of arc per century (as seen from Earth). Most of that shift could be explained by the gravitational effects exerted by other planets in the solar system. But 43 seconds of arc remained unexplained. For decades, astronomers sought a solution by searching for a postulated planet, called Vulcan, nearer to the sun than Mercury. Gravity from such a planet could explain the deviation in Mercury’s orbit. But such a planet was never found. In November 1915, Einstein used his new theory of gravity to calculate Mercury’s orbit and found that it explained the discrepancy precisely, a key argument for convincing other physicists that his theory was correct.
In the middle of the 19th century, astronomers discovered that the orbit of Mercury doesn’t quite conform to the path predicted by Newtonian gravity. On each trip around the sun, Mercury’s closest approach, or perihelion, shifts forward by a slight amount, less than 2 degrees of arc per century (as seen from Earth). Most of that shift could be explained by the gravitational effects exerted by other planets in the solar system. But 43 seconds of arc remained unexplained. For decades, astronomers sought a solution by searching for a postulated planet, called Vulcan, nearer to the sun than Mercury. Gravity from such a planet could explain the deviation in Mercury’s orbit. But such a planet was never found. In November 1915, Einstein used his new theory of gravity to calculate Mercury’s orbit and found that it explained the discrepancy precisely, a key argument for convincing other physicists that his theory was correct.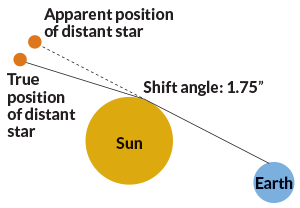
 Shortly after Einstein introduced general relativity, Karl Schwarzschild calculated its implications for the gravity of a massive sphere. Schwarzschild determined that for any given mass there existed a “critical radius” — a limit, he believed, to how small that amount of mass could be compressed. In 1939, Einstein concluded that mass could not be compressed to within that “Schwarzschild radius.” But in the same year, J. Robert Oppenheimer and Hartland Snyder calculated otherwise, claiming that a sufficiently massive object could indeed collapse within that radius, disappearing from view and leaving only its gravitational field behind.
Shortly after Einstein introduced general relativity, Karl Schwarzschild calculated its implications for the gravity of a massive sphere. Schwarzschild determined that for any given mass there existed a “critical radius” — a limit, he believed, to how small that amount of mass could be compressed. In 1939, Einstein concluded that mass could not be compressed to within that “Schwarzschild radius.” But in the same year, J. Robert Oppenheimer and Hartland Snyder calculated otherwise, claiming that a sufficiently massive object could indeed collapse within that radius, disappearing from view and leaving only its gravitational field behind.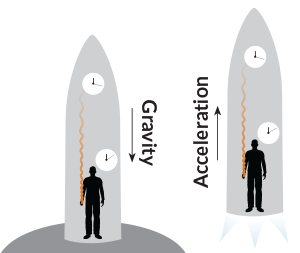 Imagine a rocket ship in free space, accelerating upward (from the perspective of an astronaut on the ship’s floor). The astronaut shoots laser pulses from the floor to a sensor on the ceiling at a rate of one per second. Because the ship is accelerating, the sensor is moving away from the laser beam during its trip to the ceiling, so the pulses arrive at intervals longer than one second. But the speed of the laser light remains constant. Therefore a clock on the ceiling must tick more rapidly than the clock on the floor to measure the speed of light accurately. Because, as general relativity requires, acceleration is equivalent to a gravitational field, the same effect should occur for laser pulses fired from the bottom to the top of a ship parked on Earth. Similarly, a clock at sea level would tick more slowly than a clock atop a mountain. This slowdown of clocks in a gravitational field is known as gravitational time dilation.
Imagine a rocket ship in free space, accelerating upward (from the perspective of an astronaut on the ship’s floor). The astronaut shoots laser pulses from the floor to a sensor on the ceiling at a rate of one per second. Because the ship is accelerating, the sensor is moving away from the laser beam during its trip to the ceiling, so the pulses arrive at intervals longer than one second. But the speed of the laser light remains constant. Therefore a clock on the ceiling must tick more rapidly than the clock on the floor to measure the speed of light accurately. Because, as general relativity requires, acceleration is equivalent to a gravitational field, the same effect should occur for laser pulses fired from the bottom to the top of a ship parked on Earth. Similarly, a clock at sea level would tick more slowly than a clock atop a mountain. This slowdown of clocks in a gravitational field is known as gravitational time dilation.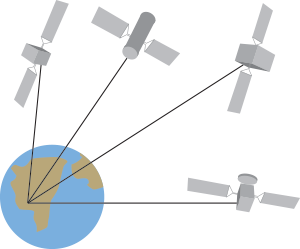 The Global Positioning System, used to pinpoint locations on the Earth’s surface, depends on signals sent from satellites orbiting about 20,000 kilometers high. A GPS receiver records the precise time that signals arrive from multiple satellites; those arrival times can be used to calculate how far away the satellites are. The receiver can then compute its own position based on the distances to the satellites and their locations. This approach requires clocks on the ground to be synchronized with clocks on the satellites. But because of gravitational time dilation, clocks on the ground run slower than those on the satellites. After just a day, your GPS would misplace your location by about 10 kilometers (six or seven miles) if the calculations weren’t corrected for relativity’s effects. (Actually, a correction is also needed for special relativity, since the satellites’ rapid motion slows their clocks. But the effect from general relativity is much greater.)
The Global Positioning System, used to pinpoint locations on the Earth’s surface, depends on signals sent from satellites orbiting about 20,000 kilometers high. A GPS receiver records the precise time that signals arrive from multiple satellites; those arrival times can be used to calculate how far away the satellites are. The receiver can then compute its own position based on the distances to the satellites and their locations. This approach requires clocks on the ground to be synchronized with clocks on the satellites. But because of gravitational time dilation, clocks on the ground run slower than those on the satellites. After just a day, your GPS would misplace your location by about 10 kilometers (six or seven miles) if the calculations weren’t corrected for relativity’s effects. (Actually, a correction is also needed for special relativity, since the satellites’ rapid motion slows their clocks. But the effect from general relativity is much greater.)