Artist Susan Happersett of Jersey City, N.J., has come up with a novel twist on the venerable Möbius strip: a playful, eye-catching creation she describes as a Möbius accordion.


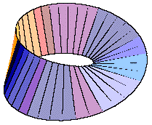

A Möbius strip, or band, is the remarkable one-sided surface that results from joining together the two ends of a long strip of paper after twisting one end 180 degrees.