Geometric arrangements of coins can serve as the basis for all sorts of puzzles. One popular variant involves going from one configuration to another by sliding coins, subject to given constraints, and doing so in the fewest possible moves.
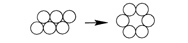
One classic puzzle, for example, starts with six coins packed tightly together in a rhomboid formation, made up of two nestled rows of three coins each. The goal is to form a ring of coins so that, if a seventh coin were placed in the center, the original six coins would be closely packed around it. The constraint is that, on each move, a coin must be slid to a new position where it touches two other coins. Can you solve the puzzle in three moves? In fact, there are precisely 24 ways to do so in three moves.
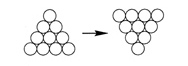
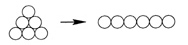
Another puzzle starts with coins arranged in a closely packed triangle. The problem is to turn the triangle upside down, sliding coins so that a single coin abuts two other coins. With a triangle of three coins, it’s possible to invert the triangle in just one move. It takes two moves to invert a triangle of six coins, and three moves to invert a triangle of 10 coins. What about 15 coins arranged in a triangle (just like the 15 balls at the start of a billiard game)?
Inverting a 15-coin triangle actually take five moves. In general, the smallest number of coins that you must move to invert a triangle can be obtained by dividing the number of coins by 3 and ignoring the remainder.
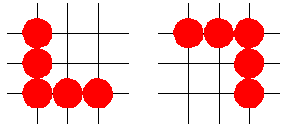
Sliding-coin puzzles in which coins are arranged in a square lattice rather than in a triangular, closely packed one and constrained to move along the lattice are much less common and present additional challenges. A common constraint is to specify that a coin must slide to a new position on the lattice that is next to at least two other coins.
Erik D. Demaine and Martin L. Demaine of the Massachusetts Institute of Technology and Helena A. Verrill of the Institut for Matematiske Fag in Copenhagen have analyzed coin-moving puzzles to determine which types of puzzles are solvable on triangular or square grids.
It turns out the most triangular-lattice puzzles are solvable. Indeed, there are only a few basic restrictions for a puzzle to be solvable. Obviously, there must be at least one valid move from the initial configuration, and the number of coins must be the same for the initial and final configurations.
Furthermore, at least one of the following four conditions must hold:
- The final configuration contains a triangle of three mutually touching coins.
- The final configuration contains four connected coins.
- The final configuration contains three connected coins and two different touching coins.
- The puzzle is solvable in a single move.
“These conditions are enough to guarantee that the puzzle is solvable,” Erik and Martin Demaine remark.
Much more stringent conditions must hold for solvable square-lattice puzzles, the researchers say. “For example, it is impossible for a configuration of coins to get outside its enclosing box. This property is quite different from the triangular lattice, where coins can travel arbitrary distances.”
Although the solvability of square-lattice puzzles is trickier to characterize, it is still possible to tell whether a given puzzle is solvable. Knowing that can be very useful for puzzle designers.
Moreover, “a surprising aspect of this work is that there is an efficient algorithm to solve most sliding-coin puzzles,” Erik and Martin Demaine say. “In contrast, most games and puzzles, when scaled up sufficiently large, are computationally intractable.”






