The game involves a set of four cubic dice, each one numbered differently. You let your opponent pick any one of the four dice. You choose one of the remaining three. Each player tosses his or her die, and the higher number wins. Amazingly, in a game involving 10 or more turns, you will nearly always have more wins.
After the first session, you can invite your opponent to pick a different die, perhaps even the one that worked so well for you. You select one of the remaining dice. Again, in a game of at least 10 throws, you’re very likely to come out the winner.
Indeed, it doesn’t matter which die your opponent picks. You can always choose another die that will practically guarantee your triumph in a game of 10 or more turns.
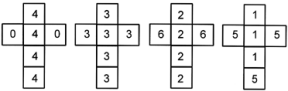
For this particular set of dice (right), the die with four 4s beats the die with six 3s, which in turn beats the die with four 2s, which beats the die with three 1s, which (completing the cycle) beats the die with four 4s!
So, it doesn’t matter which die your opponent picks. You can always choose another die that practically guarantees your triumph in a game of 10 or more turns.
Dice numbered in this fashion are known as nontransitive dice. They were designed by statistician Bradley Efron of Stanford University to help illuminate probability paradoxes that involve the violation of a mathematical property called transitivity.
In the case of the four dice shown above, the surprise arises from the mistaken assumption that the relation “most likely to win” is transitive between pairs of dice. It is not. The first die in the sequence is twice as likely to beat the second die, the second die is twice as likely to beat the third die, the third die is twice as likely to beat the fourth die, and the fourth die is twice as likely to beat the first die.
Efron came up with two additional sets of four dice that show the same nontransitive property.
SET 2: 2, 3, 3, 9, 10, 11; 0, 1, 7, 8, 8, 8; 5, 5, 6, 6, 6, 6; and 4, 4, 4, 4, 12, 12.
SET 3: 1, 2, 3, 9, 10, 11; 0, 1, 7, 8, 8, 9; 5, 5, 6, 6, 7, 7; and 3, 4, 4, 5, 11, 12.
A set of three dice can also have the same nontransitive property.
SET 4: 3, 3, 5, 5, 7, 7; 2, 2, 4, 4, 9, 9; and 1, 1, 6, 6, 8, 8.
In set 4, the first die beats the second, which beats the third, which beats the first. As it happens, this set uses all the numbers from 1 to 9. Moreover, the numbers can be written as a magic square, in which the rows, columns, and diagonals each add up to 15.
|
In the example above, each row gives the numbers for one die. Hence, the three dice all have the same total face value (30). Other magic squares also yield nontransitive dice sets.
Here’s another example of three nontransitive dice, where all the dice have the same total face value (42).
SET 5: 1, 1, 1, 13, 13, 13; 0, 3, 3, 12, 12, 12; and 2, 2, 2, 11, 11, 14.
Discovered by Allen J. Schwenk of Western Michigan University, this particular set of nontransitive dice displays an intriguing quirk when the game is changed a little. Suppose you select first, and your opponent picks second. Just for fun, the players also opt to roll each die twice, taking the total. The higher total wins.
It turns out that you would still have a winning edge, albeit a small one, even when your opponent chooses the die that would have won under the original rules.
When toy collector and consultant Tim Rowett looked for a commercial product based on nontransitive dice, he initially turned to the first set of four dice, partly because no number is greater than 6 (the highest number on a standard cubic die). Its disadvantage is that one die is all 3s. It’s not a very exciting choice for any player. You know exactly what’s going to happen with every throw.
Rowett now has a set of three nontransitive dice, where no face has a number higher than 6, and each die has two different numbers (adding a bit of suspense to the game).
SET 6: 1, 4, 4, 4, 4, 4; 3, 3, 3, 3, 3, 6; and 2, 2, 2, 5, 5, 5.
In this case, the first die beats the second in 25 out of 36 possibilities, the second beats the third in 21 out of 36 chances, and the third beats the first in 21 out of 36 tries.
As with set 5, changing the game so that your opponent picks first and both of you toss twice (or use a single throw of two identical dice), again gives you the edge.
What would happen with three rolls? r rolls? These and other variants of nontransitive dice games offer all sorts of possibilities for mathematical exploration (and for trapping the unwary).






