With two of the world’s most powerful supercomputers and a bit of mathematical sleight of hand, physicists have accomplished a longstanding and yet remarkably humble goal. They have described what happens when an electron collides with an atom.
Underlying everything from the glow of fluorescent light bulbs to the chemistry of stellar gases, such submicroscopic impacts are a cosmic commonplace. However, even after boiling down the problem to just three particles an incoming electron, the proton of the target hydrogen atom, and the atom’s own orbiting electron’ physicists have failed to describe the event in full mathematical detail.
“This is the simplest problem of impact ionization you can do, and it’s extremely difficult,” says molecular physicist Lee A. Collins of Los Alamos (N.M.) National Laboratory.
A team of California physicists describes a solution, however, in the Dec. 24, 1999 Science. “It’s a real breakthrough,” comments Collins.
It’s been nearly three-quarters of a century since physicists first wrote down the relevant quantum mechanical equation, an application of Schrödinger’s equation tailored to the collision between an electron and hydrogen. In that time, they’ve succeeded in calculating the probability of just a few types of outcomes.
For example, they’ve worked out the case where the incoming electron knocks the resident electron loose and the two fly off in exactly opposite directions, says Anthony F. Starace, a theoretical physicist at the University of Nebraska at Lincoln.
Other geometries and results have proved to be tougher mathematical nuts, Starace says. Theorists made predictions, but experimenters who fired beams of electrons into atomized hydrogen have found the estimates inaccurate.
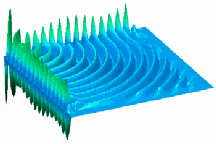
In the simpler case of an undisturbed electron orbiting a nucleus, scientists have calculated the full, detailed solution, or wave function, and from it derived the so-called orbital shapes of the electron cloud. These shapes have been a source of revolutionary insights about chemical bonding and the energy-absorption properties of atoms, says C. William McCurdy, a computational
chemist at Lawrence Berkeley (Calif.) National Laboratory and a collaborator in the solution to the collision problem. Until now, physicists had no comparable visual image for how electrons move away from a nucleus after an impact, he says.
Using supercomputers at the Berkeley and Lawrence Livermore National Laboratories, McCurdy and his colleagues calculated the wave function for the simplest such collision. The task required solving about 5 million linked equations, each containing about 5 million terms.
Only a mathematical trick kept the calculation that simple. Employed previously by others, the scheme makes the wave function shrink gradually to zero outside a sphere of a certain radius. The researchers found that the calculated wave function’s undulations settled into a pattern within that radius. This enabled them to predict its shape to infinite distance.
The theorists calculated the probabilities for different scattering outcomes using the newly derived wave function and found that the predictions agreed well with experimental data. Theoretical atomic physicist Colm T. Whelan of the University of Cambridge in England says that experimenters deserve at least half the credit for solving the collision problem since, without their detailed observations, theorists wouldn’t have been able to confirm that their recent calculations got the answer right.
With the wave function in hand, says Collins, physicists now have a benchmark against which to test potential sequences of interactions between an atom and an approaching electron.







