Normal 0 false false false MicrosoftInternetExplorer4
Take solace, all ye who’ve grown weary of carbon nanotube promises: The latest tubes are anything but nano.
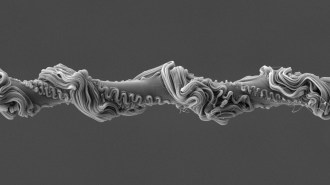
While trying to grow better, longer nanotubes, researchers accidentally discovered a new type of carbon filament that’s tens of thousands of times thicker. Christened “colossal carbon tubes,” the new structures aren’t quite as strong as nanotubes but are still 30 times stronger than Kevlar per unit weight, and are potentially easier to turn into applications, suggests a new study in an upcoming Physical Review Letters.
Though exceptionally strong, nanotubes are hard to weave into larger fibers. Labs around the world have been trying to grow longer tubes or to string tubes together because long nanotube fibers could lead to futuristic products, such as ultralight bulletproof vests or even cables that could lift cargo into space at a fraction of the cost of a rocket. But researchers have had only partial success.
Recently at Los Alamos National Laboratory in New Mexico, materials scientist Huisheng Peng and his collaborators were trying to tweak the conditions inside a vacuum oven to grow “forests” of long nanotubes from carbon gas. When Peng opened the vacuum-sealed door, he saw a scene that could be compared to the floor of a barber’s shop: Thin, black hairs were scattered everywhere.
Carbon nanotubes are not visible to the naked eye. “At first, I thought they were a lot of carbon nanotubes bonded together,” says Peng, who recently moved to Los Alamos from FudanUniversity in Shanghai, China.
Lab tests, however, revealed that the filaments, which can be centimeters long and as thick as one-tenth of a millimeter, were not clumps of nanotubes, but a new and unusual kind of structure. Using X-rays, the team found that carbon atoms form the same type of bonds in the colossal tubes as in nanotubes. The atoms are also arranged in the same hexagonal webs, which resemble chicken wire.
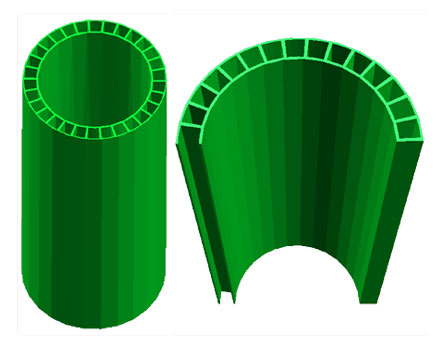
Instead of being simple cylindrical structures, the colossal tubes have two concentric layers. The researchers believe that each layer is made of many chicken wire sheets sandwiched together. Walls that are 100-nanometers thick connect the layers and divide the space between the layers into canals that run along the entire length of the tubes — similar to the gaps inside corrugated cardboard.
The colossal tubes are easily bent and stretched, and at least twice as strong as the strongest fibers made from carbon nanotubes to date, the researchers report. These tubes are also light and good electrical conductors.
László Forró of the Ecole Polytechnique Fédérale in Lausanne, Switzerland, believes that the authors may have rushed to publication with results that are too preliminary. “At this stage it is only a cookbook,” he says. “Basically, they do not know anything about the structure.”
The researchers say their tests suggest a structure similar to bundles of concentric carbon nanotubes but much larger, and with some of the chicken wire sheets broken up to leave gaps for the canals. But, Forró says, the authors’ data reveal that the chicken wire sheets are not as neatly arranged as the authors claim.
More research needs to be done, in particular to understand how the structures form and grow, admits the paper’s senior author, Quanxi Jia, of Los Alamos National Laboratory.
“What this paper does show,” says Otto Zhou of the University of North Carolina at Chapel Hill,” is that there are still a lot more new carbon materials to be discovered and explored.”