To live up to the hype, quantum computers must repair their error problems

Astronaut John Glenn was wary about trusting a computer.

It was 1962, early in the computer age, and a room-sized machine had calculated the flight path for his upcoming orbit of Earth — the first for an American. But Glenn wasn’t willing to entrust his life to a newfangled machine that might make a mistake.

The astronaut requested that mathematician Katherine Johnson double-check the computer’s numbers, as recounted in the book Hidden Figures. “If she says they’re good,” Glenn reportedly said, “then I’m ready to go.” Johnson determined that the computer, an IBM 7090, was correct, and Glenn’s voyage became a celebrated milestone of spaceflight (SN: 3/3/62, p. 131).

A computer that is even slightly error-prone can doom a calculation. Imagine a computer with 99 percent accuracy. Most of the time the computer tells you 1+1=2. But once every 100 calculations, it flubs: 1+1=3. Now, multiply that error rate by the billions or trillions of calculations per second possible in a typical modern computer. For complex computations, a small probability for error can quickly generate a nonsense answer. If NASA had been relying on a computer that glitchy, Glenn would have been right to be anxious.

Luckily, modern computers are very reliable. But the era of a new breed of powerful calculator is dawning. Scientists expect quantum computers to one day solve problems vastly too complex for standard computers (SN: 7/8/17, p. 28).

Current versions are relatively wimpy, but with improvements, quantum computers have the potential to search enormous databases at lightning speed, or quickly factor huge numbers that would take a normal computer longer than the age of the universe. The machines could calculate the properties of intricate molecules or unlock the secrets of complicated chemical reactions. That kind of power could speed up the discovery of lifesaving drugs or help slash energy requirements for intensive industrial processes such as fertilizer production.

But there’s a catch: Unlike today’s reliable conventional computers, quantum computers must grapple with major error woes. And the quantum calculations scientists envision are complex enough to be impossible to redo by hand, as Johnson did for Glenn’s ambitious flight.

If errors aren’t brought under control, scientists’ high hopes for quantum computers could come crashing down to Earth.

Fragile qubits

Conventional computers — which physicists call classical computers to distinguish them from the quantum variety — are resistant to errors. In a classical hard drive, for example, the data are stored in bits, 0s or 1s that are represented by magnetized regions consisting of many atoms. That large group of atoms offers a built-in redundancy that makes classical bits resilient. Jostling one of the bit’s atoms won’t change the overall magnetization of the bit and its corresponding value of 0 or 1.

But quantum bits — or qubits — are inherently fragile. They are made from sensitive substances such as individual atoms, electrons trapped within tiny chunks of silicon called quantum dots, or small bits of superconducting material, which conducts electricity without resistance. Errors can creep in as qubits interact with their environment, potentially including electromagnetic fields, heat or stray atoms or molecules. If a single atom that represents a qubit gets jostled, the information the qubit was storing is lost.

Additionally, each step of a calculation has a significant chance of introducing error. As a result, for complex calculations, “the output will be garbage,” says quantum physicist Barbara Terhal of the research center QuTech in Delft, Netherlands.

Before quantum computers can reach their much-hyped potential, scientists will need to master new tactics for fixing errors, an area of research called quantum error correction. The idea behind many of these schemes is to combine multiple error-prone qubits to form one more reliable qubit. The technique battles what seems to be a natural tendency of the universe — quantum things eventually lose their quantumness through interactions with their surroundings, a relentless process known as decoherence.

“It’s like fighting erosion,” says Ken Brown, a quantum engineer at Duke University. But quantum error correction provides a way to control the seemingly uncontrollable.

Make no mistake

Quantum computers gain their power from the special rules that govern qubits. Unlike classical bits, which have a value of either 0 or 1, qubits can take on an intermediate state called a superposition, meaning they hold a value of 0 and 1 at the same time. Additionally, two qubits can be entangled, with their values linked as if they are one entity, despite sitting on opposite ends of a computer chip.

These unusual properties give quantum computers their game-changing method of calculation. Different possible solutions to a problem can be considered simultaneously, with the wrong answers canceling one another out and the right one being amplified. That allows the computer to quickly converge on the correct solution without needing to check each possibility individually.

The concept of quantum computers began gaining steam in the 1990s, when MIT mathematician Peter Shor, then at AT&T Bell Laboratories in Murray Hill, N.J., discovered that quantum computers could quickly factor large numbers (SN Online: 4/10/14). That was a scary prospect for computer security experts, because the fact that such a task is difficult is essential to the way computers encrypt sensitive information. Suddenly, scientists urgently needed to know if quantum computers could become reality.

Shor’s idea was theoretical; no one had demonstrated that it could be done in practice. Qubits might be too temperamental for quantum computers to ever gain the upper hand. “It may be that the whole difference in the computational power depends on this extreme accuracy, and if you don’t have this extreme accuracy, then this computational power disappears,” says theoretical computer scientist Dorit Aharonov of Hebrew University of Jerusalem.

But soon, scientists began coming up with error-correction schemes that theoretically could fix the mistakes that slip into quantum calculations and put quantum computers on more solid footing.

For classical computers, correcting errors, if they do occur, is straightforward. One simple scheme goes like this: If your bit is a 1, just copy that three times for 111. Likewise, 0 becomes 000. If one of those bits is accidentally flipped — say, 111 turns into 110, the three bits will no longer match, indicating an error. By taking the majority, you can determine which bit is wrong and fix it.

But for quantum computers, the picture is more complex, for several reasons. First, a principle of quantum mechanics called the no-cloning theorem says that it’s impossible to copy an arbitrary quantum state, so qubits can’t be duplicated.

Secondly, making measurements to check the values of qubits wipes their quantum properties. If a qubit is in a superposition of 0 and 1, measuring its value will destroy that superposition. It’s like opening the box that contains Schrödinger’s cat. This imaginary feline of quantum physics is famously both dead and alive when the box is closed, but opening it results in a cat that’s entirely dead or entirely alive, no longer in both states at once (SN: 6/25/16, p. 9).

So schemes for quantum error correction apply some work-arounds. Rather than making outright measurements of qubits to check for errors — opening the box on Schrödinger’s cat — scientists perform indirect measurements, which “measure what error occurred, but leave the actual information [that] you want to maintain untouched and unmeasured,” Aharonov says. For example, scientists can check if the values of two qubits agree with one another without measuring their values. It’s like checking whether two cats in boxes are in the same state of existence without determining whether they’re both alive or both dead.

And rather than directly copying qubits, error-correction schemes store data in a redundant way, with information spread over multiple entangled qubits, collectively known as a logical qubit. When individual qubits are combined in this way, the collective becomes more powerful than the sum of its parts. It’s a bit like a colony of ants. Each individual ant is relatively weak, but together, they create a vibrant superorganism.

Those logical qubits become the error-resistant qubits of the final computer. If your program requires 10 qubits to run, that means it needs 10 logical qubits — which could require a quantum computer with hundreds or even hundreds of thousands of the original, error-prone physical qubits. To run a really complex quantum computation, millions of physical qubits may be necessary — more plentiful than the ants that discovered a slice of last night’s pizza on the kitchen counter.

Creating that more powerful, superorganism-like qubit is the next big step in quantum error correction. Physicists have begun putting together some of the pieces needed, and hope for success in the next few years.

Scratching the surface

Massive excitement accompanied last year’s biggest quantum computing milestone: quantum supremacy. Achieved by Google researchers in October 2019, it marked the first time a quantum computer was able to solve a problem that is impossible for any classical computer (SN Online: 10/23/19). But the need for error correction means there’s still a long way to go before quantum computers hit their stride.

Sure, Google’s computer was able to solve a problem in 200 seconds that the company claimed would have taken the best classical computer 10,000 years. But the task, related to the generation of random numbers, wasn’t useful enough to revolutionize computing. And it was still based on relatively imprecise qubits. That won’t cut it for the most tantalizing and complex tasks, like faster database searches. “We need a very small error rate … to run these long algorithms, and you only get those with error correction in place,” says physicist and computer scientist Hartmut Neven, leader of Google’s quantum efforts.

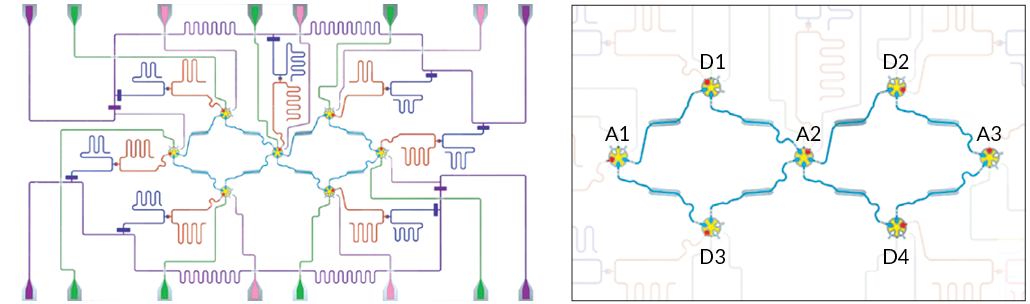
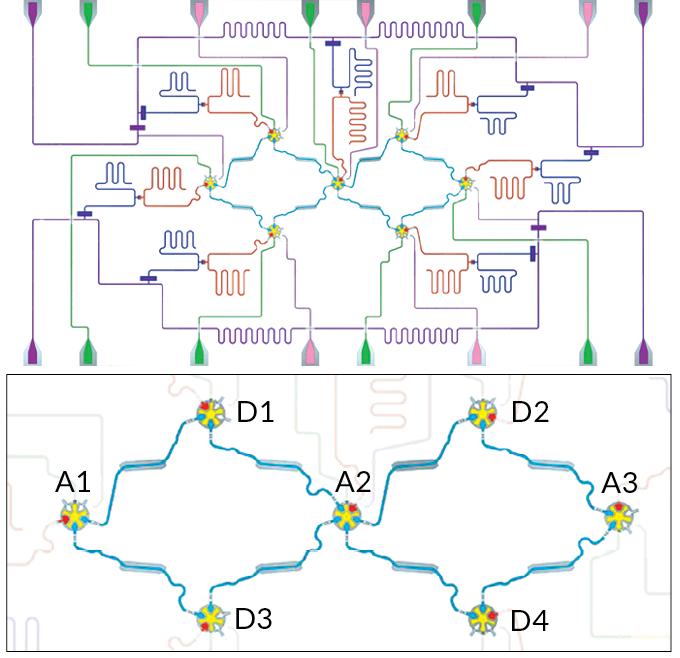
So Neven and colleagues have set their sights on an error-correction technique called the surface code. The most buzzed-about scheme for error correction, the surface code is ideal for superconducting quantum computers, like the ones being built by companies including Google and IBM (the same company whose pioneering classical computer helped put John Glenn into space). The code is designed for qubits that are arranged in a 2-D grid in which each qubit is directly connected to neighboring qubits. That, conveniently, is the way superconducting quantum computers are typically laid out.

As in an ant colony with workers and soldiers, the surface code requires that different qubits have different jobs. Some are data qubits, which store information, and others are helper qubits, called ancillas. Measurements of the ancillas allow for checking and correcting of errors without destroying the information stored in the data qubits. The data and ancilla qubits together make up one logical qubit with, hopefully, a lower error rate. The more data and ancilla qubits that make up each logical qubit, the more errors that can be detected and corrected.

In 2015, Google researchers and colleagues performed a simplified version of the surface code, using nine qubits arranged in a line. That setup, reported in Nature, could correct a type of error called a bit-flip error, akin to a 0 going to a 1. A second type of error, a phase flip, is unique to quantum computers, and effectively inserts a negative sign into the mathematical expression describing the qubit’s state.

Now, researchers are tackling both types of errors simultaneously. Andreas Wallraff, a physicist at ETH Zurich, and colleagues showed that they could detect bit- and phase-flip errors using a seven-qubit computer. They could not yet correct those errors, but they could pinpoint cases where errors occurred and would have ruined a calculation, the team reported in a paper published June 8 in Nature Physics. That’s an intermediate step toward fixing such errors.

But to move forward, researchers need to scale up. The minimum number of qubits needed to do the real-deal surface code is 17. With that, a small improvement in the error rate could be achieved, theoretically. But in practice, it will probably require 49 qubits before there’s any clear boost to the logical qubit’s performance. That level of error correction should noticeably extend the time before errors overtake the qubit. With the largest quantum computers now reaching 50 or more physical qubits, quantum error correction is almost within reach.

IBM is also working to build a better qubit. In addition to the errors that accrue while calculating, mistakes can occur when preparing the qubits, or reading out the results, says physicist Antonio Córcoles of IBM’s Thomas J. Watson Research Center in Yorktown Heights, N.Y. He and colleagues demonstrated that they could detect errors made when preparing the qubits, the process of setting their initial values, the team reported in 2017 in Physical Review Letters. Córcoles looks forward to a qubit that can recover from all these sorts of errors. “Even if it’s only a single logical qubit — that will be a major breakthrough,” Córcoles says.

In the meantime, IBM, Google and other companies still aim to make their computers useful for specific applications where errors aren’t deal breakers: simulating certain chemical reactions, for example, or enhancing artificial intelligence. But the teams continue to chase the error-corrected future of quantum computing.

It’s been a long slog to get to the point where doing error correction is even conceivable. Scientists have been slowly building up the computers, qubit by qubit, since the 1990s. One thing is for sure: “Error correction seems to be really hard for anybody who gives it a serious try,” Wallraff says. “Lots of work is being put into it and creating the right amount of progress seems to take some time.”

On the threshold

For error correction to work, the original, physical qubits must stay below a certain level of flakiness, called a threshold. Above this critical number, “error correction is just going to make life worse,” Terhal says. Different error-correction schemes have different thresholds. One reason the surface code is so popular is that it has a high threshold for error. It can tolerate relatively fallible qubits.

Imagine you’re really bad at arithmetic. To sum up a sequence of numbers, you might try adding them up several times, and picking the result that came up most often.

Let’s say you do the calculation three times, and two out of three of your calculations agree. You’d assume the correct solution was the one that came up twice. But what if you were so error-prone that you accidentally picked the one that didn’t agree? Trying to correct your errors could then do more harm than good, Terhal says.

The error-correction method scientists choose must not introduce more errors than it corrects, and it must correct errors faster than they pop up. But according to a concept known as the threshold theorem, discovered in the 1990s, below a certain error rate, error correction can be helpful. It won’t introduce more errors than it corrects. That discovery bolstered the prospects for quantum computers.

“The fact that one can actually hope to get below this threshold is one of the main reasons why people started to think that these computers could be realistic,” says Aharonov, one of several researchers who developed the threshold theorem.

The surface code’s threshold demands qubits that err a bit less than 1 percent of the time. Scientists recently reached that milestone with some types of qubits, raising hopes that the surface code can be made to work in real computers.

Getting clever

But the surface code has a problem: To improve the ability to correct errors, each logical qubit needs to be made of many individual physical qubits, like a populous ant colony. And scientists will need many of these superorganism-style logical qubits, meaning millions of physical qubits, to do many interesting computations.

Since quantum computers currently top out at fewer than 100 qubits (SN: 3/31/18, p. 13), the days of million-qubit computers are far in the future. So some researchers are looking at a method of error correction that wouldn’t require oodles of qubits.

“Everybody’s very excited, but there’s these questions about, ‘How long is it going to take to scale up to the stage where we’ll have really robust computations?’ ” says physicist Robert Schoelkopf of Yale University. “Our point of view is that actually you can make this task much easier, but you have to be a little bit more clever and a little bit more flexible about the way you’re building these systems.”

Schoelkopf and colleagues use small, superconducting microwave cavities that allow particles of light, or photons, to bounce back and forth within. The numbers of photons within the cavities serve as qubits that encode the data. For example, two photons bouncing around in the cavity might represent a qubit with a value of 0, and four photons might indicate a value of 1. In these systems, the main type of error that can occur is the loss of a photon. Superconducting chips interface with those cavities and are used to perform operations on the qubits and scout for errors. Checking whether the number of photons is even or odd can detect that type of error without destroying the data.

Using this method, Schoelkopf and colleagues reported in 2016 in Nature that they can perform error correction that reaches the break-even point. The qubit is just beginning to show signs that it performs better with error correction.

“To me,” Aharonov says, “whether you actually can correct errors is part of a bigger issue.” The physics that occurs on small scales is vastly different from what we experience in our daily lives. Quantum mechanics seems to allow for a totally new kind of computation. Error correction is key to understanding whether that dramatically more powerful type of calculation is truly possible.

Scientists believe that quantum computers will prove themselves to be fundamentally different than the computer that helped Glenn make it into orbit during the space race. This time, the moon shot is to show that hunch is right.