A century of quantum mechanics questions the fundamental nature of reality
The quantum revolution upended our understanding of nature, and a lot of uncertainty remains

Quantum theory describes a reality ruled by probabilities. How to reconcile that reality with everyday experiences is still unclear.
Max Löffler
- More than 2 years ago
Scientists are like prospectors, excavating the natural world seeking gems of knowledge about physical reality. And in the century just past, scientists have dug deep enough to discover that reality’s foundations do not mirror the world of everyday appearances. At its roots, reality is described by the mysterious set of mathematical rules known as quantum mechanics.
Conceived at the turn of the 20th century and then emerging in its full form in the mid-1920s, quantum mechanics is the math that explains matter. It’s the theory for describing the physics of the microworld, where atoms and molecules interact to generate the world of human experience. And it’s at the heart of everything that made the century just past so dramatically unlike the century preceding it. From cell phones to supercomputers, DVDs to pdfs, quantum physics fueled the present-day electronics-based economy, transforming commerce, communication and entertainment.
But quantum theory taught scientists much more than how to make computer chips. It taught that reality isn’t what it seems.

To celebrate our 100th anniversary, we’re highlighting some of the biggest advances in science over the last century. To see more from the series, visit Century of Science.
“The fundamental nature of reality could be radically different from our familiar world of objects moving around in space and interacting with each other,” physicist Sean Carroll suggested in a recent tweet. “We shouldn’t fool ourselves into mistaking the world as we experience it for the world as it really is.”
In a technical paper backing up his tweet, Carroll notes that quantum theory consists of equations that describe mathematical entities roaming through an abstract realm of possible natural events. It’s plausible, Carroll argues, that this quantum realm of mathematical possibilities represents the true, fundamental nature of reality. If so, all the physical phenomena we perceive are just a “higher-level emergent description” of what’s really going on.
“Emergent” events in ordinary space are real in their own way, just not fundamental, Carroll allows. Belief that the “spatial arena” is fundamental “is more a matter of convenience and convention than one of principle,” he says.
Carroll’s perspective is not the only way of viewing the meaning of quantum math, he acknowledges, and it is not fully shared by most physicists. But everybody does agree that quantum physics has drastically remodeled humankind’s understanding of nature. In fact, a fair reading of history suggests that quantum theory is the most dramatic shift in science’s conception of reality since the ancient Greeks deposed mythological explanations of natural phenomena in favor of logic and reason. After all, quantum physics itself seems to defy logic and reason.
Sign up for our newsletter
We summarize the week's scientific breakthroughs every Thursday.
It doesn’t, of course. Quantum theory represents the ultimate outcome of superior logical reasoning, arriving at truths that could never be discovered merely by observing the visible world.
It turns out that in the microworld — beyond the reach of the senses — phenomena play a game with fantastical rules. Matter’s basic particles are not tiny rocks, but more like ghostly waves that maintain multiple possible futures until forced to assume the subatomic equivalent of substance. As a result, quantum math does not describe a relentless cause-and-effect sequence of events as Newtonian science had insisted. Instead science morphs from dictator to oddsmaker; quantum math tells only probabilities for different possible outcomes. Some uncertainty always remains.

The quantum revolution
The discovery of quantum uncertainty was what first impressed the world with the depth of the quantum revolution. German physicist Werner Heisenberg, in 1927, astounded the scientific community with the revelation that deterministic cause-and-effect physics failed when applied to atoms. It was impossible, Heisenberg deduced, to measure both the location and velocity of a subatomic particle at the same time. If you measured one precisely, some uncertainty remained for the other.
“A particle may have an exact place or an exact speed, but it can not have both,” as Science News Letter, the predecessor of Science News, reported in 1929. “Crudely stated, the new theory holds that chance rules the physical world.” Heisenberg’s uncertainty principle “is destined to revolutionize the ideas of the universe held by scientists and laymen to an even greater extent than Einstein’s relativity.”

Heisenberg’s breakthrough was the culmination of a series of quantum surprises. First came German physicist Max Planck’s discovery, in 1900, that light and other forms of radiation could be absorbed or emitted only in discrete packets, which Planck called quanta. A few years later Albert Einstein argued that light also traveled through space as packets, or particles, later called photons. Many physicists dismissed such early quantum clues as inconsequential. But in 1913, the Danish physicist Niels Bohr used quantum theory to explain the structure of the atom. Soon the world realized that reality needed reexamining.
By 1921, awareness of the quantum revolution had begun to expand beyond the confines of physics conferences. In that year, Science News Bulletin, the first iteration of Science News, distributed what was “believed to be the first popular explanation” of the quantum theory of radiation, provided by American physical chemist William D. Harkins. He proclaimed that the quantum theory “is of much more practical importance” than the theory of relativity.
“Since it concerns itself with the relations between matter and radiation,” Harkins wrote, quantum theory “is of fundamental significance in connection with almost all processes which we know.” Electricity, chemical reactions and how matter responds to heat all require quantum-theoretic explanations.
As for atoms, traditional physics asserts that atoms and their parts can move about “in a large number of different ways,” Harkins stated. But quantum theory maintains that “of all the states of motion (or ways of moving) prescribed by the older theory, only a certain number actually do occur.” Therefore, events previously believed “to occur as continuous processes, actually do occur in steps.”
Quantum theory “is of fundamental significance in connection with almost all processes which we know.”
William Harkins
But in 1921 quantum physics remained embryonic. Some of its implications had been discerned, but its full form remained undeveloped in detail. It was Heisenberg, in 1925, who first transformed the puzzling jumble of clues into a coherent mathematical picture. His decisive advance was developing a way to represent the energies of electrons in atoms using matrix algebra. With aid from German physicists Max Born and Pascual Jordan, Heisenberg’s math became known as matrix mechanics. Shortly thereafter, Austrian physicist Erwin Schrödinger developed a competing equation for electron energies, viewing the supposed particles as waves described by a mathematical wave function. Schrödinger’s “wave mechanics” turned out to be mathematically equivalent to Heisenberg’s particle-based approach, and “quantum mechanics” became the general term for the math describing all subatomic systems.
Still, some confusion remained. It wasn’t clear how an approach picturing electrons as particles could be equivalent to one supposing electrons to be waves. Bohr, by then regarded as the foremost of the world’s atomic physicists, pondered the question deeply and by 1927 arrived at a novel viewpoint he called complementarity.
Bohr argued that the particle and wave views were complementary; both were necessary for a full description of subatomic phenomena. Whether a “particle” — say, an electron — exhibited its wave or particle nature depended on the experimental setup observing it. An apparatus designed to find a particle would find a particle; an apparatus geared to detect wave behavior would find a wave.
At about the same time, Heisenberg derived his uncertainty principle. Just as wave and particle could not be observed in the same experiment, position and velocity could not both be precisely measured at the same time. As physicist Wolfgang Pauli commented, “Now it becomes day in quantum theory.”
But the quantum adventure was really just beginning.

A great debate
Many physicists, Einstein among them, deplored the implications of Heisenberg’s uncertainty principle. Its introduction in 1927 eliminated the possibility of precisely predicting the outcomes of atomic observations. As Born had shown, you could merely predict the probabilities for the various possible outcomes, using calculations informed by the wave function that Schrödinger had introduced. Einstein famously retorted that he could not believe that God would play dice with the universe. Even worse, in Einstein’s view, the wave-particle duality described by Bohr implied that a physicist could affect reality by deciding what kind of measurement to make. Surely, Einstein believed, reality existed independently of human observations.
On that point, Bohr engaged Einstein in a series of discussions that came to be known as the Bohr-Einstein debate, a continuing dialog that came to a head in 1935. In that year, Einstein, with collaborators Nathan Rosen and Boris Podolsky, described a thought experiment supposedly showing that quantum mechanics could not be a complete theory of reality.
In a brief summary in Science News Letter in May 1935, Podolsky explained that a complete theory must include a mathematical “counterpart for every element of the physical world.” In other words, there should be a quantum wave function for the properties of every physical system. Yet if two physical systems, each described by a wave function, interact and then fly apart, “quantum mechanics … does not enable us to calculate the wave function of each physical system after the separation.” (In technical terms, the two systems become “entangled,” a term coined by Schrödinger.) So quantum math cannot describe all elements of reality and is therefore incomplete.
Bohr soon responded, as reported in Science News Letter in August 1935. He declared that Einstein and colleagues’ criterion for physical reality was ambiguous in quantum systems. Einstein, Podolsky and Rosen assumed that a system (say an electron) possessed definite values for certain properties (such as its momentum) before those values were measured. Quantum mechanics, Bohr explained, preserved different possible values for a particle’s properties until one of them was measured. You could not assume the existence of an “element of reality” without specifying an experiment to measure it.

Einstein did not relent. He acknowledged that the uncertainty principle was correct with respect to what was observable in nature, but insisted that some invisible aspect of reality nevertheless determined the course of physical events. In the early 1950s physicist David Bohm developed such a theory of “hidden variables” that restored determinism to quantum physics, but made no predictions that differed from the standard quantum mechanics math. Einstein was not impressed with Bohm’s effort. “That way seems too cheap to me,” Einstein wrote to Born, a lifelong friend.
Einstein died in 1955, Bohr in 1962, neither conceding to the other. In any case it seemed like an irresolvable dispute, since experiments would give the same results either way. But in 1964, physicist John Stewart Bell deduced a clever theorem about entangled particles, enabling experiments to probe the possibility of hidden variables. Beginning in the 1970s, and continuing to today, experiment after experiment confirmed the standard quantum mechanical predictions. Einstein’s objection was overruled by the court of nature.
Still, many physicists expressed discomfort with Bohr’s view (commonly referred to as the Copenhagen interpretation of quantum mechanics). One particularly dramatic challenge came from the physicist Hugh Everett III in 1957. He insisted that an experiment did not create one reality from the many quantum possibilities, but rather identified only one branch of reality. All the other experimental possibilities existed on other branches, all equally real. Humans perceive only their own particular branch, unaware of the others just as they are unaware of the rotation of the Earth. This “many worlds interpretation” was widely ignored at first but became popular decades later, with many adherents today.
Since Everett’s work, numerous other interpretations of quantum theory have been offered. Some emphasize the “reality” of the wave function, the mathematical expression used for predicting the odds of different possibilities. Others emphasize the role of the math as describing the knowledge about reality accessible to experimenters.
Some interpretations attempt to reconcile the many worlds view with the fact that humans perceive only one reality. In the 1980s, physicists including H. Dieter Zeh and Wojciech Zurek identified the importance of a quantum system’s interaction with its external environment, a process called quantum decoherence. Some of a particle’s many possible realities rapidly evaporate as it encounters matter and radiation in its vicinity. Soon only one of the possible realities remains consistent with all the environmental interactions, explaining why on the human scale of time and size only one such reality is perceived.
This insight spawned the “consistent histories” interpretation, pioneered by Robert Griffiths and developed in more elaborate form by Murray Gell-Mann and James Hartle. It is widely known among physicists but has received little wider popularity and has not deterred the pursuit of other interpretations. Scientists continue to grapple with what quantum math means for the very nature of reality.

It from quantum bit
In the 1990s, the quest for quantum clarity took a new turn with the rise of quantum information theory. Physicist John Archibald Wheeler, a disciple of Bohr, had long emphasized that specific realities emerged from the fog of quantum possibilities by irreversible amplifications — such as an electron definitely establishing its location by leaving a mark after hitting a detector. Wheeler suggested that reality as a whole could be built up from such processes, which he compared to yes or no questions — is the electron here? Answers corresponded to bits of information, the 1s and 0s used by computers. Wheeler coined the slogan “it from bit” to describe the link between existence and information.
Taking the analogy further, one of Wheeler’s former students, Benjamin Schumacher, devised the notion of a quantum version of the classical bit of information. He introduced the quantum bit, or qubit, at a conference in Dallas in 1992.
Schumacher’s qubit provided a basis for building computers that could process quantum information. Such “quantum computers” had previously been envisioned, in different ways, by physicists Paul Benioff, Richard Feynman and David Deutsch. In 1994, mathematician Peter Shor showed how a quantum computer manipulating qubits could crack the toughest secret codes, launching a quest to design and build quantum computers capable of that and other clever computing feats. By the early 21st century, rudimentary quantum computers had been built; the latest versions can perform some computing tasks but are not powerful enough yet to make current cryptography methods obsolete. For certain types of problems, though, quantum computing may soon achieve superiority over standard computers.
A new unit of info
Benjamin Schumacher introduced the quantum bit, or qubit, in 1992, which offers a foundation for quantum computing. The qubit can exist as both a 0 and 1. When the qubit is represented on a sphere, the angles formed by the radius to the point on the sphere determine the odds of measuring a 0 or 1.
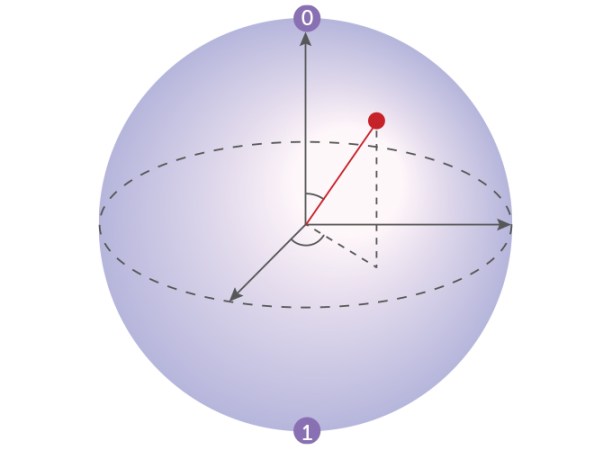
Quantum computing’s realization has not resolved the debate over quantum interpretations. Deutsch believed that quantum computers would support the many worlds view. Hardly anyone else agrees, though. And decades of quantum experiments have not provided any support for novel interpretations — all the results comply with the traditional quantum mechanics expectations. Quantum systems preserve different values for certain properties until one is measured, just as Bohr insisted. But nobody is completely satisfied, perhaps because the 20th century’s other pillar of fundamental physics, Einstein’s theory of gravity (general relativity), does not fit in quantum theory’s framework.
For decades now, the quest for a quantum theory of gravity has fallen short of success, despite many promising ideas. Most recently a new approach suggests that the geometry of spacetime, the source of gravity in Einstein’s theory, may in some way be built from the entanglement of quantum entities. If so, the mysterious behavior of the quantum world defies understanding in terms of ordinary events in space and time because quantum reality creates spacetime, rather than occupying it. If so, human observers witness an artificial, emergent reality that gives the impression of events happening in space and time while the true, inaccessible reality doesn’t have to play by the spacetime rules.
In a crude way this view echoes that of Parmenides, the ancient Greek philosopher who taught that all change is an illusion. Our senses show us the “way of seeming,” Parmenides declared; only logic and reason can reveal “the way of truth.” Parmenides didn’t reach that insight by doing the math, of course (he said it was explained to him by a goddess). But he was a crucial figure in the history of science, initiating the use of rigorous deductive reasoning and relying on it even when it led to conclusions that defied sensory experience.
Yet as some of the other ancient Greeks realized, the world of the senses does offer clues about the reality we can’t see. “Phenomena are a sight of the unseen,” Anaxagoras said. As Carroll puts it, in modern terms, “the world as we experience it” is certainly related to “the world as it really is.”
“But the relationship is complicated,” he says, “and it’s real work to figure it out.”
In fact, it took two millennia of hard work for the Greek revolution in explaining nature to mature into Newtonian science’s mechanistic understanding of reality. Three centuries later quantum physics revolutionized science’s grasp of reality to a comparable extent. Yet the lack of agreement on what it all means suggests that perhaps science needs to dig a little deeper still.







