A quarter century ago, the qubit was born
In 1992, a physicist invented a concept that would drive a new type of computing
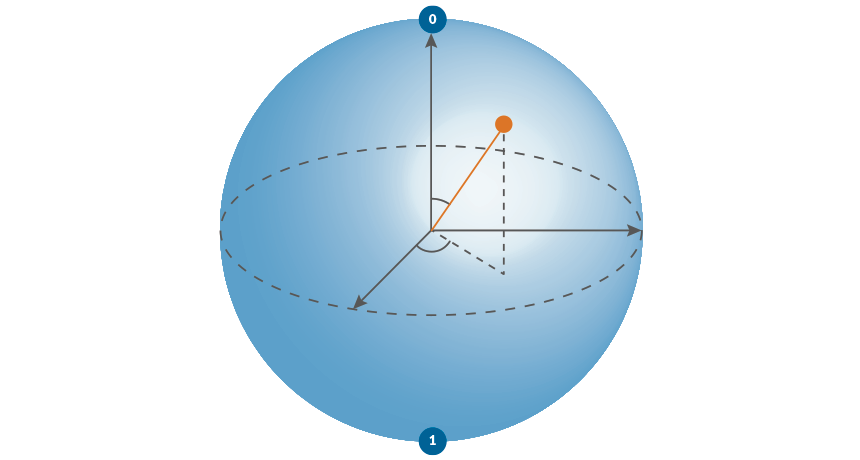
INDECISIVE INFO A qubit can exist as both a 0 and 1. When the qubit is represented on a sphere, the angles formed by the radius determine the odds of measuring a 0 or 1.
L. Lo
John Archibald Wheeler was fond of clever phrases.