Astronomers spot another star that flickers like Tabby’s star
It’s unclear what’s causing the newly discovered object to blink, but it’s probably not aliens
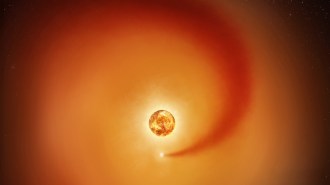
TWINKLE TWINKLE A newly identified star’s light dims irregularly, similar to Tabby’s star, shown in this artist’s illustration.
JPL-Caltech/NASA
There’s another oddly flickering star in the galaxy.
Astronomers using a telescope in Chile have discovered a star whose strange dimming and brightening of light are reminiscent of Tabby’s star, which was once suggested to host an alien megastructure.
The megastructure idea, first posited in 2015, was later quashed by data suggesting that the dips are probably from dust particles obscuring the star’s light (SN Online: 1/3/18). The new star’s behavior is probably not due to aliens, either. But it is baffling, says astronomer Roberto Saito of the Federal University of Santa Catarina in Florianópolis, Brazil. He and his colleagues reported the star’s flickering November 6 on arXiv.org.
“We don’t know what the object is,” he says. “And that’s interesting.” The star could have some sort of orbiting debris that periodically blocks the starlight, but Saito and colleagues say they need more observations to figure out if that’s possible or if the flicker is caused by something else.
The researchers had been searching for supernovas, stars that suddenly brighten as they explode, when the team spotted the object in data taken with the VISTA telescope in the Atacama Desert in northern Chile. The data were part of a larger survey of the galaxy’s center called the VISTA Variables in the Vía Láctea, or VVV.
Instead of brightening, this star suddenly dimmed. The team called it VVV-WIT-07, for “What is this?”
From 2010 to 2018, the star’s brightness waxed and waned with no set pattern. That lack of pattern is similar to Tabby’s star, except VVV-WIT-07’s light dropped by up to 80 percent, while Tabby’s star dimmed by only about 20 percent.
There’s another flickering star, J1407, that might be a closer match. That star periodically dims by up to 95 percent, astronomer Eric Mamajek of the University of Rochester in New York and colleagues reported in 2012. Astronomers think J1407 hosts an orbiting planet with an enormous ring system that periodically eclipses the star (SN: 3/7/15, p. 5).
Finding multiple stars that all dim sporadically could mean that the sources of such flickering, whatever they are, must be relatively routine, says astronomer Tabetha Boyajian of Louisiana State University in Baton Rouge, who is also Tabby’s star’s namesake.
“If this phenomenon is the same as what’s happening with Tabby’s star, then we can’t invoke an elaborate explanation for what’s happening in both systems,” Boyajian says. “If you’re starting to see stars similar to this all over the place, then it’s got to be a really common thing that happens in nature. That’s really cool.”
But she’s not yet convinced that the stars are similar.
Because VVV-WIT-07 is located in the plane of the galaxy, the view from Earth to the star is full of dust, making it hard to make out details such as the star’s distance and even what kind of star it is. If it’s a young variable star, for instance, then its light dips might be internal. Then astronomers wouldn’t need to invoke orbiting rings or other strange things.
“Pretty much everything’s on the table for it right now,” Boyajian says. “We need more data.”
Saito and his colleagues hope to follow up on the star with bigger telescopes, like the 8.1-meter Gemini telescope or the Atacama Large Millimeter Array, both in Chile.
