![]()
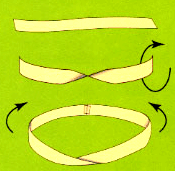
A Möbius band (or strip) is an intriguing surface with only one side and one edge. You can make one by joining the two ends of a long strip of paper after giving one end a 180-degree twist.
An ant can crawl from any point on such a surface to any other point without ever crossing an edge.
This curious object is named for the astronomer and mathematician August Ferdinand Möbius (1790–1868), a professor at the University of Leipzig. He had studied theoretical astronomy with Carl Friedrich Gauss (1777–1855) in Göttingen for two semesters early in his life and became director of the Leipzig observatory in 1848. His publications spanned a broad range of topics in both astronomy and mathematics.
In 1858, Möbius was deeply immersed in the development of a geometrical theory of polyhedra. The Paris Academy had called attention to the problem by offering a prize for its solution.
In the eighteenth century, Leonhard Euler (1707–83) had observed that in solids enclosed by plane faces, the number of vertices (V) minus the number of edges (E) plus the number of faces (F) equals 2, or V – E + F = 2. A cube, for example, has 8 vertices, 12 edges, and 6 faces: 8 – 12 + 6 = 2.
However, the formula doesn’t work for all polyhedra. For example, a polyhedron that looks like a squared-off bagel with a square hole in the middle has 16 vertices, 32 edges, and 16 faces, so V – E + F = 0.
Mathematicians were forced to consider the question of what constitutes a hole in a solid and what that has to do with Euler’s formula for polyhedra. If there were several holes, how should they be counted? What if the holes were a network of tunnels threading the solid’s interior?
Möbius identified an additional complication. In the course of his investigations, he had started to think of surfaces in terms of flat polygonal pieces glued together in various ways. If you start with a row of triangles, for instance, the strip can be twisted and joined at its ends to form a one-sided surface. He explained this remarkable one-sidedness in terms of how the triangular pieces fit together.
Möbius’s notebooks reveal that he developed this concept in September 1858. His discovery of what we now call the Möbius strip was published in 1865, in a paper titled “On the determination of the volume of a polyhedron.” In that paper, Möbius also proved that there are polyhedra to which no volume can be assigned. His essay on the theory of polyhedra, which outlined his investigations and results, was published after his death a few years later.
In one of those strange quirks of mathematical fate, Möbius was not actually the first to discover or describe the object. Credit should go to the German mathematician Johann Benedict Listing (1808–1882). Working independently, Listing first encountered the surface in July 1858. He published his discovery in an 1861 paper devoted to generalizations of Euler’s formula for polyhedra.
Nonetheless, it is the name Möbius rather than Listing that we now associate with one-sidedness. I haven’t been able to track down exactly how that came about. It’s also a bit surprising that no one before Möbius and Listing seems to have noticed the existence of one-sided surfaces.
Interestingly, the first “application” of the idea that I can find outside of mathematics is in the realm of magic.
Martin Gardner notes that the earliest known reference to the Möbius strip in the context of magic is in the 1882 enlarged English edition of Gaston Tissandier’s Les Recreations Scientifiques, first published in Paris in 1881. Magicians have long been among the earliest of adopters of new technologies and exploiters of novel scientific and mathematical ideas, all in the name of befuddling, astonishing, and mystifying their audiences.
In this parlor trick, the magician gives a spectator three large bands, each formed by gluing together the ends of a long paper strip. The magician then invites the spectator to cut each strip in half lengthwise, cutting along the strip until he or she returns to the starting point. Cutting the first band produces two, separate rings. The second forms a single band twice as long as the original. The third becomes two, interlocking rings.
What happens in each case depends on how the ends of the paper strips were joined. In the first case, there is no twist. The second is a Möbius strip, and the third is formed by twisting one end through 360 degrees before joining the ends.
Nowadays, magicians often use the term “Afghan bands” to describe the trick. That name goes back to 1904. “Why this curious name was given to the trick remains a mystery,” Gardner notes.
Discovered in a purely mathematical context, the Möbius strip is the best known of the various toys of topology. Since its discovery in the 19th century, it has also achieved a life of its own beyond mathematics–in magic, science, engineering, literature, music, and art, and in the form of the ubiquitous symbol for recycling (see Recycling Topology, September 28, 1996).
In engineering, for example, Lee De Forest obtained a 1923 U.S. patent for a Möbius filmstrip that records sound on both “sides.” The same idea was later applied to tape recorders so that a twisted tape would run twice as long as it would otherwise. Several patents have also been granted for Möbius strip conveyor belts designed to wear equally on both sides.
An object of fascination since its discovery, the Möbius strip shows up in all sorts of unexpected settings, from monumental sculptures, synthetic molecules, and postage stamps to knitting patterns and skiing acrobatics.






