The Olympic games in ancient Greece were part of a major religious festival honoring the god Zeus. Every 4 years, men from every corner of the Greek world gathered for several days of celebrations, athletic contests, and ceremonies. The term olympiad refers to the 4-year interval between Olympic games by which time was reckoned in ancient Greece. Inevitably, the games attracted vendors, traders, sculptors, poets, writers, and others—all presenting varied wares to sell to or entertain the many spectators.

The Olympic games were not the only athletic contests in ancient Greece. The Pythian games took place at Delphi every 4 years, 2 years after the Olympic games. These games had started off as music contests in honor of the god Apollo, but by 582 B.C., they also included athletic events. The festivities lasted 6 to 8 days and featured various cultural activities. Musicians and actors competed to be the best in playing the flute, singing, or reciting tragedy.
In that spirit, modern-day Olympic Games have included a variety of cultural events. This year, as Athens prepared for the latest edition of the Olympic Games, the Hellenic Mathematical Society hosted the 45th International Mathematical Olympiad (IMO), July 6–18.
Held annually since 1959, the IMO brings together teams of high school students from around the world to compete in solving extremely challenging math problems. This year’s competition in Athens featured six-student teams from 85 countries.
Over the course of 2 days, the competing students had 9 hours to solve six problems.
In the final team standings, China took first place, followed by the United States and Russia. It was the best U.S. showing since 1994.
The IMO also awarded 45 gold medals to the students who managed to “correctly and elegantly” solve all six problems.
Overall, the U.S. team earned five gold medals and one silver medal. Oleg Golberg of Bedford, Mass., earned a gold medal and 40 out of 42 possible points, obtaining the best score on the U.S. team. The other gold-medal winners were Tiankai Liu of Saratoga, Calif., (38 points), Aaron Pixton of Vestal, N.Y., (37 points), Alison Miller of Niskayuna, N.Y., (33 points), and Tony Zhang of Arcadia, Calif., (33 points). Miller was the first female gold-medal winner for a team from the U.S. Matt Ince of Arnold, Mo., earned 31 points and a silver medal.
Interestingly, Tiankai was a member of the 2001 U.S. IMO team. That team’s efforts are vividly described in Steve Olson’s book Count Down. He also participated in the 2002 IMO. Tiankai has a Web site at http://www.geocities.com/buniakowski/.
How would you do at the IMO? You can find a list of questions (and solutions) featured at these competitions since 1959 at http://www.kalva.demon.co.uk/imo.html.
Here’s a geometry problem from this year’s set of questions.
Let ABC be an acute-angled triangle with AB not equal to AC. The circle with diameter BC intersects the sides AB and AC at M and N respectively. Denote by O the midpoint of the side BC. The bisectors of the angles BAC and MON intersect at R. Prove that the circumcircles of the triangles BMR and CNR have a common point lying on the side BC.
Next year’s IMO will take place in Cancun, Mexico.
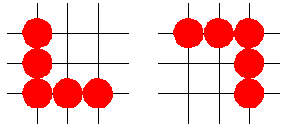
Puzzle of the Week
You have five pennies arranged on a square grid so that they all touch at least one other penny and form an “L” (above left).
Move the pennies one at a time to invert the “L” (above right), making sure that on each move a penny always ends up in a new position on the grid where it touches at least two other pennies.
Can you do it? If so, how many moves does it take?
For a hint, a Java applet to try the puzzle, or the answer, go to http://www.sciencenewsforkids.org/articles/20030723/PuzzleZone.asp.






