Most complete map of Titan reveals connected seas and cookie-cutter lakes
Latest Cassini data help fill in details about Saturnian moon’s surface
NORTHERN LAKES Radar images of Titan’s poles show lakes that may form like Earth’s sinkholes. A new topographic map suggests these hydrocarbon lakes may be connected through Titan’s equivalent of groundwater.
JPL-Caltech/NASA, ASI, USGS
Liquid methane and ethane flow through a subterranean plumbing system on Titan, which drains lakes and connects seas. That’s one of the first scientific results from the latest, most complete map of the Saturnian moon’s topography.
Planetary scientist Paul Corlies of Cornell University and colleagues released the map — based on all the data from NASA’s Cassini mission, which ended in September (SN Online: 9/15/17) — in Geophysical Research Letters on December 2.
Titan, Saturn’s largest moon, hosts seas, lakes, clouds and rain — all composed of hydrocarbons such as methane and ethane instead of water. The elevations of seas and mountains across 9 percent of Titan’s surface were directly recorded by Cassini as it flew past Titan over 13 years. The researchers had to infer altitudes for the rest of the globe.
Compared with previous maps, the new one adds mountains in the southern hemisphere and shows that Titan is more of a squashed sphere than previously thought. Researchers can now use the map to build computer simulations of everything from Titan’s atmosphere to its interior structure. “Within hours of the paper actually being available online, people we’ve never collaborated with started contacting [Corlies] to ask how to get the data,” says study coauthor Alexander Hayes, a planetary scientist also at Cornell.
But the first study to use the map, also published December 2 in Geophysical Research Letters, is research that Hayes has been working on for a decade. The work shows that Titan has a sea level as well as the hydrocarbon equivalent of groundwater — pores in subsurface rock are filled with liquid that can seep into and between the lakes and seas.
“Looking for actual evidence that the lakes could be communicating was a fundamental question from Cassini,” Hayes says. “This is the final paper that gives the best evidence that it exists.”
His team analyzed the altitudes of Titan’s liquid bodies and found that the three largest seas — Ligeia Mare, Kraken Mare and Punga Mare— are all about the same elevation, just like Earth’s oceans. In other words, Titan has a sea level, Hayes says. To maintain that uniformity, the seas must be connected through channels that could be above or below ground.
Story continues after graph
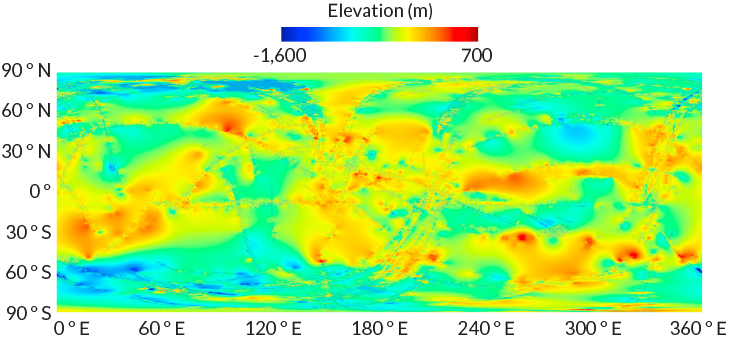
Around the globe
A new map of Titan’s topography, made with data from the Cassini mission to Saturn, shows mountains (redder colors) as well as seas and depressions (bluer colors).
The moon’s poles are dotted with small lakes and depressions that are shaped like lakes but contain no liquid. Hayes and colleagues found that the liquid levels of the filled lakes are above sea level, so they are potentially isolated from the seas. If the lakes and seas were connected, the lakes’ liquid could drain into the seas, and the liquids’ surface heights would all match — or the lakes would be empty.
The floors of the dry lake beds are at a higher elevation still. Hayes thinks that may indicate that their liquid flowed into the filled polar lakes. Those hydrological connections probably occur underground because there do not appear to be enough connections on the surface. If scientists could dig deeper into a dry lake, he predicts, they would hit liquid at the level of the filled lakes’ surfaces.
A remaining mystery is how the small polar lakes formed. Both the dry and filled lakes have steep walls, flat floors and rims that rise above the surrounding ground — features that lakes on Earth tend not to have. “They look like you went around Titan’s polar region with a cookie cutter and cut out little shapes,” Hayes says.
His best guess is that the lakes are sinkholes (SN: 1/25/14, p. 14), which collapsed when the bedrock material was dissolved out from under them. If true, then Titan’s poles may be covered with a thick layer of a kind of solid that hydrocarbons can dissolve, like acetylene. But sinkholes shouldn’t have raised rims, so that theory doesn’t explain everything.
The researchers hope other investigators will have some new ideas. “We’re just saying, these are all the observations. Please tell us how they fit together,” Hayes says.
Planetary scientist Jani Radebaugh of Brigham Young University in Provo, Utah, thinks the odd lakes could be the remnants of icy volcanoes. Explosive eruptions could create the raised rims, and the depressions could be empty magma chambers that collapsed. “I think we should consider it,” she says.
But she agrees that Hayes’ groundwater theory makes sense. Seeing hydrological systems on Titan that are similar to Earth’s “is satisfying, and helps to validate that what we understand from the Earth should work on other bodies, regardless of what the liquid is made of,” she says.
