Have you ever wondered why the cover of a manhole is nearly always round? Why isn’t it oval or square?

The usual answer is that a circular lid, unlike a square or an oval cover, won’t fall through the opening. There’s no way to position a round lid so that it can slip through a slightly smaller hole of the same shape. That’s because a circle has a constant diameter. It is the same width all the way around.
In contrast, an oval or an ellipse is longer than it is wide. You can always find a way to slip an oval lid through a hole of the same shape. That’s also true of a square or a hexagonal cover.
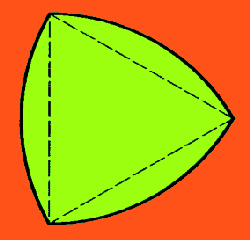
Amazingly, the circle isn’t the only shape that would work safely as a manhole cover. In fact, any shape of constant width would do, and there are infinitely many such shapes. The simplest example is the Reuleaux triangle, named after distinguished mechanical engineer Franz Reuleaux (1829–1905), who was a teacher in Berlin more than 100 years ago.
One way to draw a Reuleaux triangle is to start with an equilateral triangle, which has three sides of equal length. Draw three arcs of circles, with each arc having as its center one of the triangle’s corners and as its endpoints the other two corners. The resulting “curved triangle,” as Reuleaux termed it, has a constant width equal to the length of the interior triangle’s side.
This shape, with rounded corners, may be familiar as the cross section of a bottle of NyQuil or Pepto-Bismol. Its most prominent and successful application may well be in the Wankel rotary internal combustion engine, which once powered several types of cars manufactured by Mazda and still survives in the Mazda RX-Evolv prototype sports car. The engine featured a curved, triangular rotor turning in a specially shaped housing.
Like a circle, a Reuleaux triangle fits snugly inside a square having sides equal to the curve’s width no matter which way the triangle is turned. Indeed, the rounded triangle can rotate freely inside the square. Interestingly, as it rotates, the curved figure traces a path that eventually covers nearly every part of the square. This property is the basis for an ingenious rotary drill that, constrained by a special guide plate, bores square holes.
It’s possible to construct a curve of constant width not only from an equilateral triangle but also from any polygon with an odd number of sides. Thus, you can readily obtain a curved pentagon, heptagon, and so on. Some coins have a rounded heptagonal shape that allows their use in slot machines designed for ordinary coins.
The Reuleaux curves described so far have corners–points where two sides meet at an angle. However, curves of constant width having rounded corners can be readily constructed from the angular forms. Moreover, a curve of constant width need not be symmetrical or even consist of circular arcs. Therefore, an unlimited number of curves of constant width are possible, and the Reuleaux triangle happens to be the family member of least area.
Why can’t Reuleaux polygons be used in place of wheels? The trouble is that these polygons dont have a fixed center of rotation. The hub of a circular wheel, for example, stays a fixed height above the ground, allowing smooth, horizontal motion. In contrast, the center of, say, a Reuleaux triangle, wobbles as the curve rotates. That doesn’t matter for rollers laid down on a surface to ease the passage of a heavy load, but it does matter if the roller or wheel has a fixed axis.
Francis C. Moon, a professor of mechanical and aerospace engineering at Cornell University in Ithaca, N.Y., has taken a close look at Franz Reuleaux and his work. One of Reuleaux’s special interests was kinematics–the mathematical description of motion.
In developing a catalog of mechanisms that could be combined to create new machines, Reuleaux focused on the various ways in which machines convert one motion into another. A steam locomotive, for example, is a machine that converts the reciprocating motion of a piston into the rotation of its driving wheels.
Cornell has a collection of more than 200 mechanical models based on designs created by Reuleaux to illustrate his ideas. The university purchased the models in 1882 to serve as teaching aids in the training of mechanical engineers.
Moon notes that the Reuleaux triangle predates Reuleaux. “It was used as a positive return cam in early steam engines,” Moon says. Cornell’s mechanism collection includes a model of such a device.
To this day, Reuleaux triangles and their constant-width siblings remain objects of fascination in the classroom and elsewhere.
Originally posted: 10/19/96
Updated: 9/20/03






