Small Infinity, Big Infinity

Infinity is bigger than any number. But saying just how much bigger is not so simple. In fact, infinity comes in infinitely many different sizes—a fact discovered by Georg Cantor in the late 1800s.

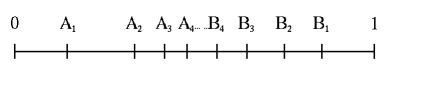
Now a mathematician has come up with a new, different proof. Based on a simple game, the proof uses a strategy that might someday shed light on one of the great unsolved questions in mathematics.

The smallest infinity is the one you’d get to if you could count forever. The numbers 1, 2, 3, 4… are called the natural numbers, and they are the most obvious example of this size of infinity. In honor of them, anything that has this size of infinity is called “countable.”

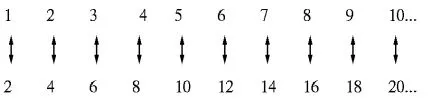
Lots of infinite things are countable. For example, suppose you take just the even numbers. They’re countable, just like all the natural numbers are. You can prove it by counting them:

This leads to the peculiar result that, in some sense, there are the same number of even numbers as there are of all the natural numbers—even though there are only half as many. Infinity is an odd beast.

Cantor also came up with a clever way to count all the fractions, proving that they’re also countable. So there are (in a sense) just as many fractions as whole numbers, too! (To see why, go to http://www.homeschoolmath.net/.)

Not everything infinite is countable, though. Take, for example, all the real numbers—all the counting numbers plus all the fractions plus all the irrational numbers. A real number is any number that can be expressed in decimals, though the expression might continue forever. For example, pi is a real number: It can be written as 3.14159….

What Cantor showed was that no matter what clever counting scheme you come up with, you’ll never manage to count every last real number. He did it with a challenge: Just try it. Come up with a counting scheme, any counting scheme, and he’ll find a real number you missed.

He reasoned this way. He would write down all your numbers in a list, including only the portion after the decimal point. If the number was rational, he would write it with an infinite number of zeros at the end, or the numbers would start repeating in an infinite loop. The list would look something like this, though it probably wouldn’t be these particular numbers:

.48859283404162…

.23190734486346…

.23987932750000…

.34576128733518…

.23758093475639…

etc.

Now Cantor would cook up a new number that wouldn’t be anywhere in your list. To find the first digit, he would look at the first digit of the first number, which in this case is a 4. Cantor would make the first digit of his new number something different, say 5.

Now he would look at the second digit of the second number, in this case, 3. He’d make the second digit of his new number something different, say 4. And he’d make the third digit of his new number different from the third digit of the third number in the list (which is 9, so he could make his 0).

By keeping this up forever, he’d get a new real number that was different from every other number in your list. After all, it can’t be the same as the first number, because it has a different first digit. And it can’t be the same as the second number, because it has a different second digit. For the same reason, it can’t be the same as any of the numbers in the list. So he’s got you! You didn’t count every last real number after all.

Cantor’s discovery raised a question that hasn’t been fully answered even today: Is there a “medium” size of infinity—bigger than the natural numbers but smaller than the real numbers? The supposition that nothing is in between the two in size is called the “continuum hypothesis,” after the continuum of numbers. The question is so puzzling that it led to a genuine crisis in mathematics, and mathematicians still aren’t sure of the answer.

When mathematicians get stuck on a problem like this, they usually need a new approach. Using a method entirely different from Cantor’s, Matthew H. Baker of the Georgia Institute of Technology in Atlanta recently came up with a new proof that the real numbers aren’t countable. Baker started by considering a little mathematical game. Let’s say that Alice and Bob decide on some subset of the real numbers between 0 and 1. Alice starts by picking any number she likes between 0 and 1, and Bob follows by choosing a number that is bigger than Alice’s but still less than 1. Then they take turns picking new numbers that are always between the last two numbers chosen.

If we call Alice’s numbers A1, A2, A3, etc., and Bob’s B1, B2, B3, etc., we can draw a picture that would look something like this:

Notice that Alice and Bob’s picks get closer and closer to each other over time. An important theorem in calculus says that if they were to keep picking numbers this way forever, Alice’s numbers would get closer and closer to just one single number, which will be bigger than all the An‘s and smaller than all the Bn‘s.

So that brings us to the point of the game. Remember at the beginning that Alice and Bob agreed on some subset of the interval. If the number Alice converges toward is in that subset, Alice wins, and if it’s outside, then Bob wins.

Baker found a strategy that Bob can use to win anytime the subset is countable. Bob can make a list of all the numbers in the subset: S1, S2, S3, etc. Bob has to make sure that Alice’s numbers can’t converge toward any number on that list.

For his first pick, he looks at S1. If S1 is smaller than A1, he doesn’t have to worry about Alice’s numbers converging toward it, because he knows Alice’s numbers have to converge toward something bigger than any of them. So he just picks any number he feels like that is allowed.

If S1 is bigger than A1, he can just pick S1! After all, he also knows Alice’s numbers can only converge toward something smaller than all of his numbers. By making each of his choices this way, he can make sure that Alice’s numbers can’t converge toward any point in the subset.

But then Baker noticed something else. If the subset that Alice and Bob agreed on at the beginning was the entire interval from 0 to 1, Bob obviously couldn’t win. But if the subset were countable, Bob could win. So that implies that the whole interval can’t be countable.

Baker says his proof doesn’t show anything Cantor didn’t, but that it’s a nice example of how two areas of mathematics that don’t seem to have much to do with one another—in this case, game theory and set theory—are in fact tightly linked. Hard problems in mathematics are often solved by bringing together fields of math that seem only distantly related.

Indeed, set theorists are pursuing game theory approaches. “People take some of these games seriously because they can give non-trivial insights into the nature of real numbers,” Baker says. “They may be able to shed light on things like the continuum hypothesis.”

---

If you would like to comment on this article, please see the blog version.