A Twist on the Möbius Band
Researchers work out the shape of a paper strip
- More than 2 years ago
A Möbius band is a two-dimensional surface with the puzzling property of having only one side. Despite this mind-bending characteristic, it’s an easy object to make: just take a long strip of paper, give one end a half-twist, and tape the two ends together. Because of the half-twist, the front side of one end of the strip joins with the reverse side of the other end, so that the taped-together band has only one side.
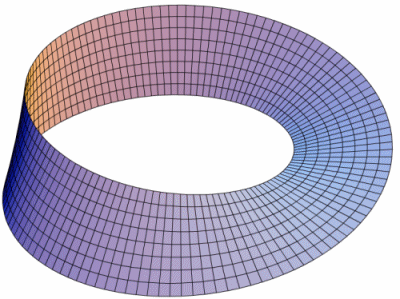

When you do that, precisely what shape do you get? Until very recently, oddly enough, no one had come up with a complete answer. If the material is elastic, describing the shape is straightforward. Imagine holding a circular ring (with no thickness) and placing the midpoint of a stick at any point on it, perpendicular to the plane of the circle. Now move the stick around the circle—either direction will do—and at the same time rotate it smoothly lengthwise so that by the time it returns to its starting place, it has flipped through 180°. The shape it sweeps out in this maneuver is a Möbius band.
By contrast, a flat, non-stretchy band, such as a strip of paper, can’t quite assume this shape. Try it: The center line of a paper Möbius strip becomes a kind of hilly racetrack, closer to an oval or a triangle than a circle, and it swoops up and down. Furthermore, the paper doesn’t twist smoothly throughout its whole length. Instead most of its 180-degree rotation occurs in a few short, separate sections. The wider the strip of paper, the less circular the Möbius band and the more abruptly the paper twists. Mathematicians have worked out approximate descriptions for paper (or other non-stretching) Möbius bands, but until recently, no one had a precise formula for the shape.
“This is an old problem,” says mechanical engineer Evgueni Starostin of University College London. “It’s a very simple question, but it turns out that it requires a rather good theory” to solve it. Starostin and his colleague Gert Van der Heijden have now found the solution and have published their results online for an upcoming Nature Materials.
They solved the problem by imagining that the paper was like a band made of stiff, springy metal that was resistant to bending. The shape of the Möbius strip, they proved, was the one that required the least amount of energy to bend.
The researchers originally became interested in the problem while trying to understand the shapes that DNA takes as it twists. Like paper, DNA won’t stretch. Like a metal strip, it is stiff and resists bending. The Möbius band served as a simplified model that allowed them to develop their technique for calculating possible DNA shapes.
If you would like to comment on this article, please see the blog version.






