Critter-finding mission to Antarctica’s Larsen C iceberg scrapped
Too much ice prevented the research vessel from reaching the calving site
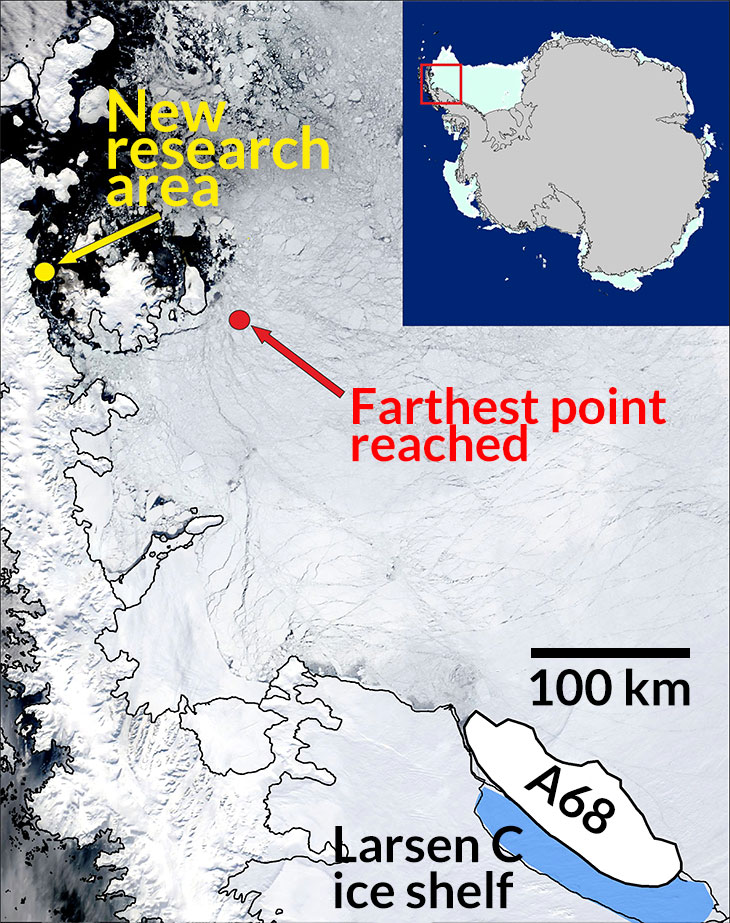
PACKED ICE Floating ice — 4- or 5-meters-thick in some places — choking the Weddell Sea ended a British Antarctic Survey research vessel’s mission to the Larsen C ice shelf in February. The mission planned to explore seafloor life newly exposed after a giant iceberg split off from the shelf last July.
Susie Grant/BAS
This article is only available to Science News subscribers.
Subscribers, enter your e-mail address to access our archives.
