Algebraic Hearts

One of the marvels of mathematics is the way in which an austere equation can unexpectedly blossom into an appealing geometric shape when represented graphically.

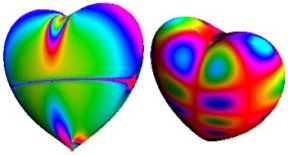
I can still recall experiencing such a sense of wonder when, decades ago, I first learned about polar coordinates in a high-school trigonometry class. In those days, there were no graphing calculators (or even pocket calculators), and all plotting was done by hand, point by point, on sheets of graph paper.

I found it fascinating to see wonderful curves and patterns slowly emerge from arrays of painstakingly plotted points. Plotting an equation expressed in terms of angle and radial distance on exotic graph paper added to the allure. It was also fun trying to predict what a seemingly slight change in an equation would do to the resulting figure.

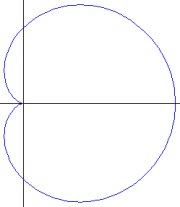
One pleasant surprise was the unveiling of graceful polar curves known as limaons from the deceptively simple equation r = b + acosq. For the special case of b = a, the result is a two-dimensional heart-shaped curve known as the cardioid. For other combinations of a and b, the closed curve either is dimpled or has a loop.

Curiously, a heart-shaped figure also comes up in mapmaking. Many people are familiar with the Mercator projection, which maps positions on a globe onto a rectangular grid–enabling a map of the world to fit neatly on an atlas page. The so-called Bonne projection maps points on a sphere onto an area that resembles the shape of a heart (see http://mathworld.wolfram.com/BonneProjection.html). Like all projections, this one preserves some features of the original global geometry but distorts others.

Equations that yield three-dimensional heart-shaped surfaces are harder to find.

Gabriel Taubin of the IBM Thomas J. Watson Research Center in Yorktown Heights, N.Y., encountered one in the late 1980s while working on a doctoral thesis involving computer vision. He was using algebraic curves and surfaces to model solid objects for recognition purposes. “Because it was difficult to visualize the results, I got interested in algorithms to rasterize algebraic curves and surfaces,” Taubin says. In effect, he wanted efficient procedures for determining which cells, or pixels, of a grid of square cells (say, on a computer monitor) correspond to a given curve.

The algorithms that Taubin developed worked well even in the vicinity of cusps and other singularities. “I discovered the equation of the heart while trying to construct surfaces with complex singularities,” Taubin says.

A heart surface has several singularities, including a sharp point at the bottom and a deep indentation at the top. Here’s Taubin’s equation for a three-dimensional algebraic heart: (x² + (1.5)²y² + z² – 1)³ – x²z³ – (1.5)²/20 y²z³ = 0.

Eric Weisstein of Wolfram Research provides nearly the same sextic equation and a visualization of this heart surface at http://mathworld.wolfram.com/HeartSurface.html. Given the equation, it’s possible to generate a variety of heart surface representations.

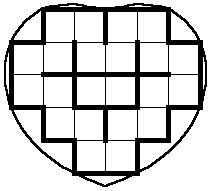
Here’s a final heart-y treat. Ed Pegg Jr. of Champaign, Ill., has invented a little puzzle involving prime numbers and a grid of squares that fits snugly within a heart. Fill in the grid, one digit per square, using each of the 21 two-digit prime numbers (11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97) just once. When filled in, the numbers read from top to bottom and from left to right. Prime numbers may share squares, but do not cross the solid lines.

“The number of love, at the center, is unique,” Pegg says. However, there are more than 100 ways to fill in the remaining squares.

One possible solution will appear at the end of next week’s MathTrek article.