Some mathematical problems are easy to describe but turn out to be notoriously difficult to solve. Nonetheless, despite their reputed difficulty and repeated warnings from those who had failed to solve them in the past, these infamous problems continue to lure mathematicians into hours, days, and even years of futile labor.
In a presentation this week on “mathematical problems between order and chaos,” Jeffrey C. Lagarias of AT&T Labs–Research highlighted three such notorious unsolved problems. His was a cautionary tale, aimed at an audience that included 12 high-school students who had already shown their problem-solving proficiency by topping the 2002 U.S.A. Mathematical Olympiad (USAMO).
Susceptible himself to the lure of these tantalizing conundrums, Lagarias admitted that he could have subtitled his talk “some problems I wish I could solve.” In recent years, Lagarias has made important research contributions in a variety of mathematical fields, including work on the randomness of pi’s digits, number patterns related to circles nested within circles, and the problem of distinguishing knots from unknots.
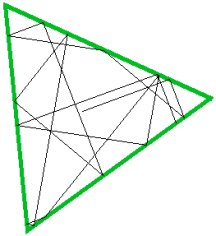
Billiards in triangles
In a game of mathematical billiards, a ball moves across a table of a given shape at a constant speed forever. There’s no friction to slow the ball down. It simply travels in a straight line until it hits a cushion and rebounds according to the rule that the angle of reflection equals the angle of incidence.
What makes the game interesting is the table’s geometry. Depending on the ball’s initial position and direction, its path after repeated reflections can vary considerably within the confines of tables having different shapes. For example, on a circular table, a ball can follow paths that never penetrate an inner circular region of a certain diameter in the middle of the table. A stadium-shaped table leads to unpredictable paths reminiscent of chaos.
In the case of tables bounded by straight lines, one unsolved problem concerns triangular tables: Is it true that every triangular table has a periodic orbit–in other words, a billiard-ball path that repeats itself?
In the case of triangles in which all three interior angles are acute, the answer is known to be “yes.” In 1992, Michael D. Boshernitzan of Rice University hinted that there may exist some sort of polygon (or triangle) that has no periodic orbit. However, no one has yet pinned down its identity–if it actually exists.
Kolakoski sequence
A Kolakoski sequence is a string of numbers that describes itself. Such a sequence is formed from a pair of one-digit numbers, m and n. When m = 1 and n = 2, the resulting sequence is made up of “blocks” of single and double 1s and 2s, where a block is a single digit or a pair of digits different from the digit or pair of digits in the preceding block.
To construct the sequence, start with the single digit 1 (the first block). The single 1 means that a block of length one follows the initial block. Because the first block is 1, the second block must be 2 to give the two-block sequence 12.
Now, the single 2 of the second block means that the third block has length two, so 11 is added to the sequence to give 1211. The addition of two 1s means that the fourth and fifth blocks each have length one, giving first 12112 and then 121121. The addition of 21 means that the sixth block has length two and the seventh block length one: 121121221.
Kolakoski sequence (first 42 digits):
K = 121121221221121122121121221121121221221121. . . .
Here are some unanswered questions about this mysterious sequence.
Is there a formula for the nth term?
If a certain string (for example, 21221) occurs in the sequence, must it occur again?
If a certain string (for example, 21221) occurs in the sequence, must the same digits in reverse order (12212) also occur?
If a certain string (for example, 21221) occurs in the sequence, must a new string in which 1 and 2 are swapped (12112) also occur?
In the long run, do as many 1s occur as do 2s? In other words, is the limiting frequency of 1s precisely 0.5? So far, Vasek Chvatal has been able to show that the limiting frequency is between 0.499 and 0.501.
Intriguingly, a variant of the Kolakoski sequence involving the digits 1 and 3 may shed light on describing where atoms are located in unusual materials known as quasicrystals.
The 3x + 1 conjecture
The so-called 3x + 1 conjecture has baffled mathematicians for more than 70 years. Also known as the Collatz problem, it concerns a sequence of positive integers.
Start with any positive integer n.
If n is even, divide it by 2 to give n’ = n/2.
If n is odd, multiply it by 3 and add 1 to give n’ = 3n + 1.
For example, starting with 5, you get the following sequence: 5, 16, 8, 4, 2, 1, 4, 2, 1,. . . .
Starting with 11, you get the sequence: 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1,. . . .
The numbers generated by these rules are sometimes called “hailstone numbers” because their values fluctuate wildly up and down (as if suspended in turbulent air) before they finally crash (to the ground) as the repeating string 4, 2, 1.
Computational experiments suggest that such a sequence will always eventually crash. However, for some starting integers, it takes a huge number of steps to reach the repeating cycle.
Will you always end up in a repeating cycle? No one has yet found a counterexample. Computation has verified that no such counterexample can start with an integer less at least 1015.
Other questions concerning the 3x + 1 sequence have proved equally elusive.
Between order and chaos
All three examples fall within an area of mathematics known as dynamical systems–which deals with the evolution over time of systems such as groups of planets or sets of billiard balls moving according to certain rules.
“These are dangerous problems,” Lagarias warned his audience at the National Academy of Sciences ceremony that honored the 2002 USAMO winners. Attempting them can be risky to your health and career.
Lagarias also offered the following “advice” about deciding which mathematical problems are worth pursuing.
Question: How can you tell whether a problem is hopelessly difficult?
Answer: Judgment.
Question: How do you develop good judgment?
Answer: Good judgment comes from experience; experience comes from bad judgment.
The 2002 USAMO top scorers were Daniel M. Kane of Madison, Wisc., Ricky Ini Liu of Newton, Mass., Tiankai Liu of Exeter, N.H., Po-Ru Loh of Madison, Wisc., and Inna Zakharevich of Palo Alto, Calif., all of whom wrote perfect papers. The other winners were Steven J.F. Byrnes of Lexington, Mass., Michael A. Hamburg, South Bend, Ind., Neil Peder Herriot of Palo Alto, Calif., Anders H. Kaseorg of Charlotte, N.C., Alison B. Miller of Niskayuna, N.Y., Gregory Price of Falls Church, Va., and Tong-ke Xue of Chandler, Ariz.
Hamburg received a special award, presented by the Clay Mathematics Institute (see http://www.claymath.org/awards/cmiolympiadscholar/2002/hamburg2002.htm), for the most original and correct solution to one of the six problems in this year’s contest. Here’s the problem he solved:
I have an n x n sheet of stamps, from which I’ve been asked to tear out blocks of three adjacent stamps in a single row or column. (I can tear only along the perforations separating adjacent stamps, and each block must come out of a sheet in one piece.) Let b(n) be the smallest number of blocks I can tear out and make it impossible to tear out any more blocks. Prove that there are real constants c and d such that, for all n > 0,
1/7 n2 – cn b(n) n2 + dn.
Hamburg’s handwritten answer. Problem proposer’s solution.
Hamburg also won the award for the most original solution to a contest problem last year.
After a demanding summer training program at the University of Nebraska in Lincoln, six of the 12 U.S. Olympiad winners will compete as the U.S. team in the International Mathematical Olympiad (IMO) to be held July 19-30 in Glasgow, Scotland.
It’s too early to tell whether any of the Olympiad winners will succumb to the lure of the “dangerous problems” that Lagarias described.






