A frustrating view of complexity

In the 1980s, an inkling emerged among some scientists that very disparate phenomena might on some deep level be related. The weather, protein folding, computers, evolution, the stock market, the immune system … each shows complex behavior arising from fairly simple interactions among its parts.

For the past 20 years, researchers have labored to understand how these and other “complex systems” work. But there’s still no agreement about even the most basic of questions: What is a complex system?

The frustration of this enduring question has led one researcher to a new answer: Frustration itself lies at the heart of complexity. A complex system, argues Philippe Binder of the University of Hawaii at Hilo, is one with an inner conflict. Conflicting tendencies built into the system won’t let the tendencies settle into a steady state.

Imagine, for example, three atomic magnets that can spin up or down. Suppose the particles are arranged in a triangle, and that each magnet is required to spin in the opposite direction of its two neighbors. Unfortunately, no arrangement meets this goal. So in such a system, the particles would flip their spins over and over in complex patterns, frustrated by the conflicting demands and never able to settle into a stable configuration.

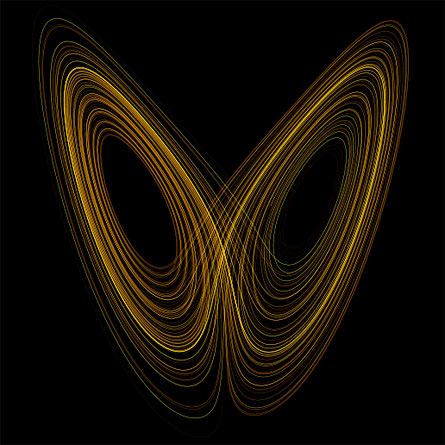
Binder believes that this notion can unite the competing definitions of complexity that have arisen in recent decades. Take, for example, Edward Lorenz’s famous “butterfly” attractor, one of the earliest examples of a chaotic system studied. A simple equation, applied repeatedly, moves points in a plane to new points. As the points move, they trace out two loops that look like a butterfly’s wings. Track a single point, and you’ll find something odd: It doesn’t move in an orderly fashion between the two wings, rather it bounces between them in a seemingly random pattern. Furthermore, two points that start close to one another can easily get pulled to opposite sides of the butterfly, ending up nowhere near one another.

This is a complex system, some would say, because it’s impossible to predict the path of a point unless you know with infinite precision where it was to begin with. Binder says that while that captures an element of what it means to be a complex system, what underlies the unpredictability is frustration. The equation of the Lorenz attractor has combined tendencies to both compress and to stretch the plane.

Another perspective on complex systems is that their fundamental attribute is that they behave differently on different scales. DNA, for example, functions very differently from an entire human cell, which in turn doesn’t act much like an organ or a whole person. An eddy that overall moves clockwise may have small sub-eddies that turn counterclockwise. The needs of an individual may be at odds with the needs of society as a whole. Binder describes this as “scale frustration.”

The third form of complexity people often talk about is computational complexity. Many phenomena can be translated into a sequence of 0s and 1s in some way. For example, a point whirling around the Lorenz butterfly can generate such a sequence if you keep track only of which wing it’s on. Then scientists can figure out what the simplest computer is that could generate that sequence.

Noam Chomsky defined a hierarchy of theoretical computing machines, with the most complex being what is called a “universal Turing machine.” Such a machine is equivalent in complexity to a modern computer and is capable in theory of computing anything that can be computed.

Remarkably, though, there are some sequences a Turing machine can’t compute at all. A computer that tries will keep computing forever, never coming to a final answer. Phenomena that generate such strings could be considered the most complex of all.

“That’s the ultimate example of dynamical frustration,” Binder says. “You cannot answer the question, you keep going around in circles, never stopping.” The computer is caught between the need to come to an answer and the need to follow the rules of its program.

Binder admits that his work is preliminary. “It’s still a half-baked idea,” he says, “but I hope it will bring a little focus to the discussion.” He’s now working to make the connections rigorous.

David Wolpert, a physicist at NASA Ames Research Center in Moffett Field, Calif., says that Binder is on to something. Self dissimilarity, he says, is at the heart of complexity. Such phenomena may be common, he says, because it is efficient: If you think of a system as embodying a kind of computation, then he notes that self-dissimilar systems break that computation up, performing different portions of it at different scales, like a parallel computer.

Binder says that the situation in complexity science is a bit like the blind men feeling the elephant: The description given by the person feeling the trunk would seem totally incompatible with that of the person feeling the belly. Binder hopes his notion of dynamic frustration may help identify the full animal. “I think it might be more like a platypus than an elephant!”