Chemicals in biodegradable food containers can leach into compost
Long-lasting PFAS compounds could end up in plants that are later eaten by people

PERSISTANT PFAS A worrisome class of chemicals called PFAS are found in some compostable food containers and many other consumer items like nonstick cookware. The compounds can leach out of the containers and build up in compost.
Igoriss/iStock/Getty Images Plus
Composting biodegradable food containers cuts the amount of trash that gets sent to a landfill. But the practice may serve up some unintended consequences for human health.
That’s because the items often contain perfluoroalkyl and polyfluoroalkyl substances, or PFAS, to help repel water and oil. These persistent chemicals can leach out of the packaging and end up in compost, researchers report May 29 in Environmental Science & Technology Letters. When that compost is used, PFAS could be taken up by plants and ultimately accumulate in the bodies of people, though the health effects are still unclear.
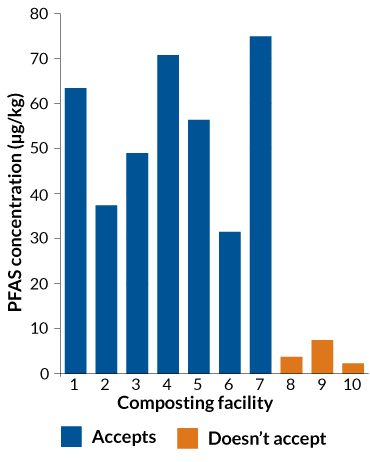
The scientists measured perfluoroalkyl acids, or PFAAs, a subset of PFAS formed by microbial degradation, in compost from 10 commercial facilities. Seven of these facilities accepted compostable food containers, and three didn’t. With the food containers in the mix, the team measured PFAAs at concentrations from about 29 to 76 micrograms per kilogram of compost, while compost from facilities that didn’t accept the containers contained less than 8 micrograms PFAAs per kilogram of compost.
“There was a huge difference in the PFAS levels between those two groups,” says Laurel Schaider, an environmental chemist and public health researcher at Silent Spring Institute in Newton, Mass., not involved in the study. People expect the things they compost to break down entirely and become a sustainable source of nutrients for plants, so it’s concerning that chemicals in compostable items can persist, she says.
As a class, PFAS include thousands of compounds, many with useful properties. They show up in flame-retardant carpets, in nonstick coatings on cookware and myriad other places. “Everybody’s happy to have all those conveniences, but the trade-off … is pretty huge because [the compounds] don’t go away,” says Linda Lee, an environmental fate chemist at Purdue University in West Lafayette, Ind. Microbes can usually help break down chemicals in general, but for this persistent bunch, the organisms typically transform the compounds into other PFAS.
A chain of carbon forms the backbone of PFAS to which fluorine atoms are attached. Lee and colleagues found that most of the PFAS in compost samples were shorter-chain ones rather than more notorious, longer-chained perfluorooctanoic acid, or PFOA, and perfluorooctanesulfonic acid, or PFOS, which have been largely phased out in the United States. Shorter-chain PFAS don’t hang out as long in the body as their longer cousins, but they can more easily move from organic material in soil to water and be taken up by plants.
Studies have linked PFAS to negative health effects including high cholesterol, lowered fertility and birth weight, as well as testicular and kidney cancer, Schaider says. But only a handful of PFAS, including PFOS and PFOA, have been thoroughly investigated for their potential health effects. Little is known about how most of the ones detected in the compost samples affect human health.
The researchers analyzed the compost because Washington state was concerned that it might have been a mistake to allow composting of food containers. In part because of the team’s results, the state passed the Healthy Food Packaging Act, which bans PFAS in paper food packaging beginning in 2022 if the state can find something to replace the compounds.
“It’s a really strong study,” says Jennifer Guelfo, an environmental engineer at Texas Tech University in Lubbock not involved in the research. With this information on which PFAS show up in compost, scientists can start to figure out what health risks might be associated with those chemicals, and if the chemicals should be used in this type of packaging at all, she says. “Now is the time to look at the uses of these compounds … and limit their uses to those scenarios where they are absolutely needed.”