Computer programs can handle all sorts of data, from sums of money in bank accounts to sensor readings from scientific instruments. In many cases, the data are a set of discrete elements, such as temperatures. Moreover, some elements of a set may be larger in value than others, or they may exhibit some other relationship that allows you to rank them or put them in order.

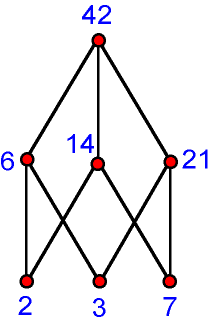
In mathematics, such a collection of elements is known as a partially ordered set, or poset. One example of a poset consists of an integer and all its positive divisors (excluding 1). For instance, the positive divisors of 42 are 2, 3, 6, 7, 14, and 21. The relationships among the integers in the poset {2, 3, 6, 7, 14, 21, 42} can be expressed symbolically in a special type of diagram known as a Hasse diagram, named for mathematician Helmut Hasse (1898–1979).
A Hasse diagram consists of dots, which represent the elements of a set; and connecting lines, which represent the relationships among the elements. For a poset including the divisors of a given integer, the integer itself would be at the top of the diagram and its prime factors would be at the bottom.
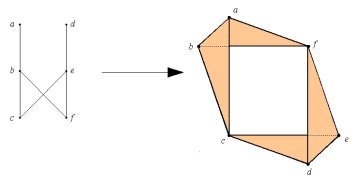
Research involving a link between posets and geometric figures was the focus of an award-winning project in the 2001 Intel Science Talent Search. Gabriel D. Carroll, a student at Oakland Technical High School in Oakland, Calif., titled his project “Homology of Narrow Posets.” His work was based on the fact that, for a given a poset (often expressed as a Hasse diagram), it’s possible to construct a geometric object that encodes the same relationships among the elements as the poset itself.
Studying such geometric objects can provide insights into the corresponding posets, just as studying posets can provide insights into the corresponding geometric objects, Carroll notes.
|
Hasse diagram for a given poset and its corresponding geometric figure.
|
Carroll studied posets visualized as complex collections of angular forms known as simplexes. A triangle is an example of a two-dimensional simplex, and a tetrahedron is an example of a three-dimensional simplex. His goal was to relate fundamental geometric characteristics of these simplicial complexes (sets of simplexes) to some intrinsic property of the posets themselves.
Carroll focused on a characteristic of simplexes described by the term homology. Roughly speaking, homology refers to the types of closed paths that go from one corner to the next of an angular geometric figure (a simplicial complex). Fundamentally different geometric figures will have different paths, or homologies.
Carroll computed so-called homology groups for various simplicial complexes, then he looked for patterns and eventually conjectured and proved certain results. In technical terms, he obtained an upper bound for the sizes of a complex’s homology groups in terms of a poset property called width.
“Thus, if a poset is ‘simple,’ as measured by its width, its complex will also be ‘simple,'” Carroll concludes.
Carroll’s study won third place in the 2001 Science Talent Search. He had had no previous experience in the field of algebraic topology but had cheerfully delved into the topic when it was suggested by graduate student Tilman Bauer of the Massachusetts Institute of Technology. Bauer was Carroll’s mentor at the Research Science Institute 2000, held at MIT.
“I approach any problem with a wide array of tools,” Carroll notes. “There are general problem-solving strategies, such as examination of special cases, phrasing problems in alternate language, looking for extremal situations, or using induction. . . .I also have an arsenal of theorems that can accelerate my work, and, having solved thousands of problems over the last few years, I often recognize similarities with past problems that suggest how to attack the problem at hand.”
He adds, “Perhaps the most useful single mathematical tool is an open mind.”
Carroll has been a member of two U.S. Mathematical Olympiad teams. He enjoys playing the piano, debating, writing poetry, and programming computers.
“The value of much of mathematics. . .is cultural,” Carroll remarks. “It is a form of art; it provides exercise for the mind.”






