A pursuit curve is the path an object takes when chasing another object. Such a path might result from a fox pursuing a rabbit or a missile seeking a moving target.
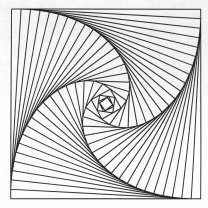
More formally, a pursuer must always head directly toward the pursued, and the pursuer’s speed must be proportional to or match that of the pursued. Plotting the lines of sight at regular intervals and tracing out the corresponding paths can produce fascinating patterns.
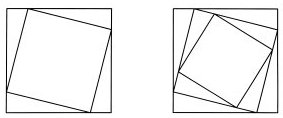
Pursuit curves can arise in a variety of situations and may involve more than one pursuer. Suppose that a person stands at each corner of a square traced out on the ground. Each person looks directly at the person to his or her left, then begins to walk toward that person. If all four people move at the same time and at the same constant speed, each person follows a spiral path toward the square’s center.
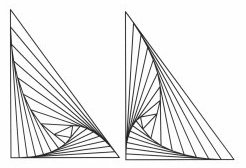
The following recipe for drawing pursuit curves works with squares and other regular polygons:
1. Draw a regular polygon. One pursuer starts off at each corner of the polygon.
2. Mark the spot on each side of the polygon that each pursuer has reached after a fixed period of time.
3. Join the new points to show the new chasing directions and create a new polygon.
4. On the new polygon, mark off the same length from each corner as you did for the original polygon and join the resulting points to create another, smaller polygon.
5. Continue in the same fashion until you can’t comfortably fit a new polygon into the remaining area.
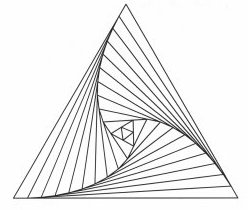
In the case of a square, it’s possible to mimic the resulting pattern by constructing a series of larger and larger right-angled triangles, starting with a square in the middle. Such an arrangement of triangles and squares can serve as the basis for a colorful, eye-catching quilt.
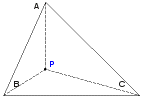
When three pursuers start at the corners of an equilateral triangle, they meet at a point in the middle of the triangle. This meeting spot is known as a Brocard point, named for French army officer Henri Brocard (1845–1922). In general, a triangle has two Brocard points. In the equilateral case, the two points coincide.
A Brocard point has the property that lines drawn from the vertices to the point are inclined at the same angle to each side of the triangle.
Interestingly, Brocard found the points now named for him in the course of studying the problem of three dogs chasing one another. Instead of focusing on what happens in an equilateral triangle with all three dogs moving at the same speed, he looked at a more general case involving triangles that are not equilateral. However, he still wanted the dogs to meet at the same time and at the same point (the Brocard point). This meant the dogs had to run at different speeds along their spiral paths. Moreover, there were two possible sets of spiral paths, one set for each Brocard point.
Interestingly, for paths converging to a Brocard point, the successively smaller triangles remain the same shape from one snapshot to the next. If the speeds were kept constant, the triangles would change shape in successive snapshots.
The rules for drawing pursuit curves and their variants can serve as recipes for creating artistic designs. Pursuit curves offer many artistic possibilities, says English educator and artist John Sharp. They also have links to some very high-level mathematics, he notes.
Next week: Art of Pursuit.






