Ripples race in the brain as memories are recalled
People were more likely to remember a word if their brains buzzed with a spike of activity
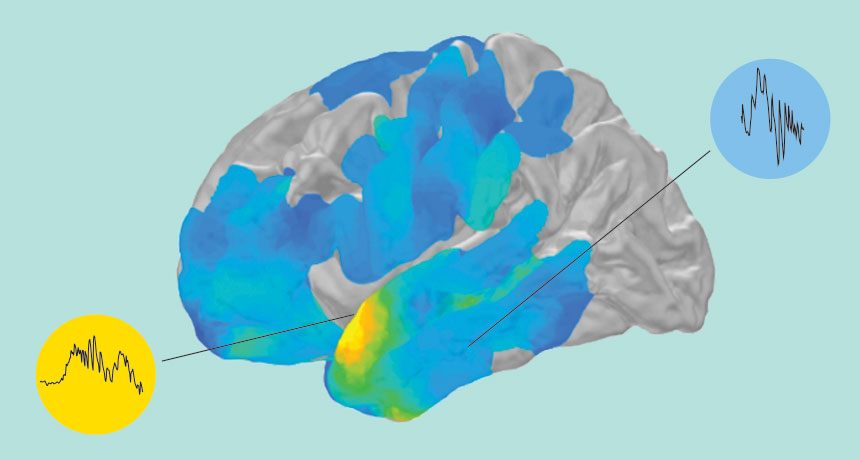
TANDEM WAVES Just before people remembered a word, fast ripples of brain activity happened simultaneously in two areas, the temporal association cortex (yellow) and the medial temporal lobe (blue).
N. CARY/SCIENCE