Dip a flat wire ring into a basin of soapy water. The ring comes out spanned by a taut, iridescent soap film in the form of a thin disk. Its area is smaller than it would be if the surface had peaks and valleys, or even small wrinkles. A clinging soap film invariably settles into the shape that mathematicians call a minimal surface. They can also imagine minimal surfaces that don’t exist in nature.

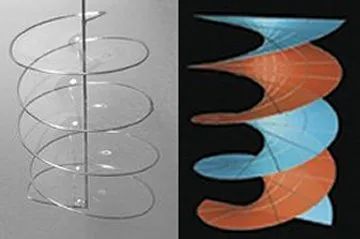


Consider a perfectly flat disk of soap film, for example, that extends so far over the horizon that its boundary can’t be seen. This two-dimensional plane is the simplest example of a minimal surface that is infinite in extent and not an endless repetition of some basic shape.
Mathematicians can also imagine twisting that plane to produce another infinite shape called the helicoid. Also a minimal surface, it looks like a pair of intertwined spiral slides—a double helix—at its core and it stretches away to infinity as a stack of sheets.
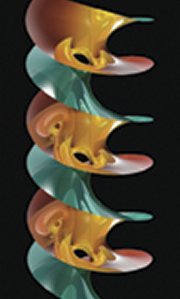
For centuries, the plane and the helicoid were the only known examples of infinite, unbounded minimal surfaces that don’t fold back to intersect themselves. Then, in the early 1990s, mathematicians discovered a new minimal surface that seemed to have the same basic properties that the helicoid has, but with a crucial difference: Through one of its sheets, it has a tunnel (SN: 10/24/92, p. 276). Topologists refer to such an opening as a handle, in deference to a favorite everyday shape, a coffee mug.
Although computer images and other evidence strongly suggested that the new surface met the criteria for placing it, alongside the helicoid and the plane, in the minimal-surface hall of fame, that wasn’t enough for mathematicians. “No matter how good the computer approximations are, you can never be sure just by computer,” says Frank Morgan of Williams College in Williamstown, Mass.
So, mathematicians sought an airtight proof that the infinite surface doesn’t somehow, somewhere, twist around enough to intersect itself.
Matthias Weber of Indiana University in Bloomington, David Hoffman of Stanford University, and Michael Wolf of Rice University in Houston now offer a proof that nearly settles the question. Their work, published in the Nov. 15 Proceedings of the National Academy of Sciences, establishes that a particular shape—a helicoid with a handle—doesn’t intersect itself. The only remaining subtlety is to show that this surface and the helicoid with a handle discovered in the 1990s are one and the same.
Disk covery
At every point, a minimal surface is either flat, like a disk, or has a saddle shape. In the latter case, its curvature resembles that of a potato chip, which typically starts out as a flat, thin slice of moist potato. As a chip loses water during frying, it shrinks. Minimizing its area, it curls into a saddle shape.
Twisting the ordinary two-dimensional plane into a helicoid converts the plane’s flatness into saddle-based curviness. Topologists classify the helicoid as a “complete embedded minimal surface of finite topology with infinite total curvature.” The word embedded indicates that the surface doesn’t fold back on itself. Complete means that it extends indefinitely and has no boundary.
In the early 1990s, David Hoffman and Fusheng Wei, then at the University of Massachusetts at Amherst, and Hermann Karcher of the University of Bonn in Germany discovered complicated equations that seemed to represent a surface just like the helicoid but with a tunnel penetrating one of the levels. Computer-generated images provided tantalizing glimpses of this novel surface.
Hoffman shows animations of the new surface to audiences by starting at a spot far above the hole and sliding downward. Morgan says, “After a while, the audience is sure it’s just the helicoid, when suddenly the unexpected hole appears.”
That wasn’t the only surprise. The team had actually identified an infinite family of minimal surfaces, each characterized by a different number of handles. It appeared that the new sort of helicoid could have any number of tunnels and still qualify as the same sort of minimal surface as the basic helicoid and the plane. The mathematicians, however, had great difficulty proving that the helicoid with a handle and all its cousins don’t somehow intersect themselves.
For the vexing problem of whether a surface folds back on itself, the complex equations characterizing minimal surfaces mask more than they reveal. Computer visualizations of the equations help but can’t provide a complete answer.
“The problem in much of the research that we are doing lies in determining the interplay of the algebraic nature of the formulas with the geometry and topology of the shapes these formulas represent,” Weber says.
Constructing such a surface is like piecing together local maps in an atlas to create a detailed map of the world. “You know how the map on page 27 fits with the maps on pages 25, 26, and 28, but the maps on pages 27 and 62 might just cross each other,” Wolf says. “This makes it quite difficult to detect global properties of the shape.”
Genus one
In the rubbery world of topology, it’s possible to imagine creating a helicoid by carefully deforming and stretching the surface of a punctured sphere rather than by expanding and twirling a flat soap film. You’d stretch the rim of the sphere’s puncture hole to infinity to create a plane and then twist the plane into the double spiral characteristic of the helicoid.
Putting a tunnel in the helicoid is equivalent to adding a handle—just like the one that sprouts from a coffee mug—to a punctured sphere. Mathematicians call the result a genus-one helicoid.
Several years ago, William H. Meeks III of the University of Massachusetts and Harold Rosenberg of the Université Denis Diderot in Paris proved that a complete, embedded minimal surface that was topologically a punctured sphere with no handles had to be either the basic helicoid or the plane. In other words, “there’s only one helicoid with no handles,” Wolf says. Meeks and Rosenberg built their proof on earlier investigations of the structure of minimal surfaces done by Tobias Colding of New York University and William Minicozzi of Johns Hopkins University in Baltimore.
The new proof by Weber, Hoffman, and Wolf establishes that a helicoid with one handle doesn’t fold back on itself. Originally, in one special case, Hoffman, Wei, and Karcher had proved that a helicoid with an infinite number of handles—a hole at each level of an infinite tower—exists and doesn’t intersect itself. Weber and Wolf later developed a new way of thinking about minimal surfaces that enabled Weber to provide an alternative, much simpler and shorter, proof that this surface with infinitely many handles is embedded.
By manipulating equations, Weber, Hoffman, and Wolf then carefully deformed this particular surface so that it always stayed free of intersections, even as the number of handles decreased. To do so, they took advantage of a particular property of the helicoid.
One can construct a plane by lifting a horizontal line upward with a constant speed, Weber says. If one simultaneously rotates the line with a constant speed around a fixed vertical axis, one obtains the basic helicoid. Decreasing the rotational speed of the line while still moving the horizontal line upward corresponds to stretching out, or “untwisting,” the ordinary helicoid. The process of untwisting pushes the handles vertically farther and farther apart, until finally, at the limit, there’s a helicoid with just one handle. In effect, all the other handles are twisted away. (See http://www.msri.org/about/sgp/jim/geom/
minimal/library/helicoidg1p/index.html.)
In this way, Weber, Hoffman, and Wolf reached the genus-one helicoid, establishing that it, too, is embedded. The proof shows that helicoids with more than one handle are also embedded.
The entire proof, which runs to more than 100 manuscript pages, contains just mathematical logic and prose. None of the argument requires computer calculations or visualizations.
Nonetheless, “our understanding of what must be going on was aided by pictures, animations, hand drawings, and all manner of geometric and visual thinking,” Hoffman says. “The process here is to pin down what really is correct without reference to unverifiable intuition and common belief.”
There’s still the delicate matter of the relationship between the surface characterized by the proof and the one-handle surface that Hoffman, Wei, and Karcher constructed more than a decade ago. “Whether it is the same surface is not yet known,” Hoffman says. “More generally, we do not know, but do believe, that there is only one embedded surface with [the relevant] properties.”
Future flexibility
Recent advances related to the structure of minimal surfaces and new ways of representing them promise many more developments in the realm of soap-film mathematics. Weber, for one, is interested in what happens when handles on a helicoid are squeezed together instead of being twisted away.
“Sheer curiosity forces us mathematicians to figure out what’s going on in this limit as well,” Weber says.
Weber and Martin Traizet of the Université François Rabelais in Tours, France, have recently produced intriguing images of compressed helicoids. “The resulting limit is quite surprising and can be described as a ‘parking-garage structure,’ a term we coined for this phenomenon,” Weber says.
A typical real-life parking garage can be thought of as a giant helicoid, with two spiral ramps, one for driving up and the other for coming down. These ramps can involve a sequence of either right turns or left turns. The new minimal structure found by Weber and his team is like a three-ramp parking garage, with two spirals turning left and one spiral turning right. To further complicate the picture, the parking levels are close to each other.
Inspired by computer-generated images, Weber and Traizet have proved that it’s possible to construct families of minimal surfaces using such parking-garage structures—in effect, by gluing together helicoids laterally. These surfaces, in turn, may be related to helicoids with some finite number of handles.
The various directions of current research on minimal surfaces suggest a rich future full of amazing forms. Mathematicians will need new insights to organize and classify the members of this burgeoning zoo.
Wolf says, “The times are exciting because we are partly there, but still at the stage where we don’t know if we are nearly there or only a few steps down the path.”






