Benjamin Franklin Plays Sudoku

Only in the last five years has sudoku been capturing people’s recreational time. But 250 years ago, Benjamin Franklin was developing fascinating puzzles with principles quite similar to sudoku, keeping himself occupied while taking a break from his electrical investigations. Now, a mathematician has discovered two Franklin puzzles even more fantastic than those previously known and written a book describing all of Franklin’s mathematical endeavors.

In Benjamin Franklin’s Numbers: An Unsung Mathematical Odyssey (Princeton University Press, 2007), Paul C. Pasles of Villanova University in Pennsylvania argues that Franklin’s mathematical achievements have long been overlooked. Franklin applied common-sense quantitative reasoning in many areas where it had never been used—for example, calculating the economic costs of war and slavery, and making population forecasts before the field of population demographics had been developed.

But his mathematical inclinations come out most dramatically in his “most devious magic squares, odd little amusements that must have required considerable facility with number relationships,” Pasles writes.

A 3-by-3 magic square is a grid of the numbers 1 through 9 arranged so that every row, column, and diagonal adds up to the same number.

Magic squares can be made larger as well. A 4-by-4 magic square, for example, uses the numbers 1 through 16. Unlike sudoku, magic squares don’t require any special properties of subgrids—though Franklin created some squares that have them as well.

A myth dates the original magic square to 2200 B.C., when a turtle is said to have emerged from the Lo River in China with a pattern of markings on its back corresponding to a 3-by-3 magic square. Just as sudoku would spread around the world thousands of years later, so magic squares spread to Tibet, Japan, Thailand, Europe, Africa, and finally America. Franklin probably first encountered magic squares in a 1708 book on recreational mathematics.

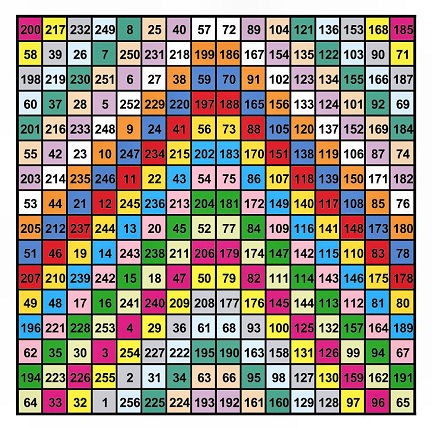
As with other aspects of his life, Franklin developed clever innovations in magic squares. “Not being content with these [regular properties of magic squares], which I looked on as common and easy things, I had imposed on myself more difficult tasks, and succeeded in making other magic squares, with a variety of properties, and much more curious,” Franklin wrote in a letter. For example, in this 8-by-8 magic square Franklin created, each color-coded pattern adds up to 260.

This magic square is filled with many other similar hidden patterns as well.

When a friend of Franklin’s mentioned having seen an impressive 16-by-16 magic square, Franklin refused to be outdone.

Each row, column, and chevron-shaped “bent row” in Franklin’s 16-by-16 magic square adds up to 2056. In addition, if you choose any 4-by-4 subgrid within the magic square and add up the numbers, you’ll get 2056 as well!

Delighted by his own efforts, Franklin dashed off another letter: “This I sent to our friend the next morning, who after some days, sent it back in a letter, with these words:— ‘I return to thee thy astonishing or most stupendous piece of the magical square, in which’—but the compliment is too extravagant, and therefore, for his sake, as well as my own, I ought not to repeat it. Nor is it necessary; for I make no question you will readily allow this square of 16 to be the most magically magical of any magic square ever made by any magician.”

But still, the magician strove to out-magic himself. He devised a new game, a “magic circle of circles.”

The numbers along each radius of the circle add up to 360, and each of the concentric circles of numbers also adds up to 360. In addition, the numbers along each colored circle also add up to 360. The following diagram shows how Franklin drew the colored “excentric” circles.

Pasles found a hidden connection between Franklin’s magic squares and magic circles. Imagine taking one of Franklin’s squares and moving the rows around into a circle, spreading it out like a fan. Then the rows would turn into the radii of a magic circle, while the columns would turn into the circumferences drawn in black. But what of Franklin’s idiosyncratic bent rows? They, Pasles deduces, become the excentric circles!

Despite Franklin’s wizardry, his magic squares seemed to all lack one key feature: their diagonals don’t sum to the right number. Critics declared them inferior, their magic tarnished. Franklin claimed in a letter to have created a magic square with both diagonals and bent rows summing correctly, but no record of such a square was known.

Now Pasles has found two magic squares Franklin created that each contains all of the various properties. A 16-by-16 square turned up in a facsimile of a letter that had previously been overlooked, and an 8-by-8 magic square appeared in an early translation of a letter. Pasles shows both magic squares in his new book.

Pasles says that while Franklin’s mathematics stayed in the realm of simple arithmetic arguments, its importance shouldn’t be dismissed. Franklin was involved in the foundations of decision science, statistics, demographics, and other areas, and his magic squares and circles show a remarkable ingenuity. “Those inspired moments are as much a part of mathematics as the really heavy stuff,” Pasles says.

---

If you would like to comment on this article, please see the blog version.