Here’s why mathematicians are so interested in cake cutting
The problem attracts game theorists, computer scientists, economists and more

The cake serves as a metaphor for anything that can be divided, like land, time or limited resources.
MADELINE MCMAHON
- More than 2 years ago
Read another version of this article at Science News Explores
Ariel Procaccia has thought a lot about how to cut cake over the last 15 years. That’s partly because the Harvard computer scientist has three children who among them have celebrated more than two dozen birthdays. He knows what it’s like to stand with a knife before a layered masterpiece, frosted with buttercream and chocolate curls, while pressed on all sides by small partygoers who instinctively recognize when someone else gets a better slice.
But it’s also because much of Procaccia’s work focuses on exploring the mathematical rules for dividing stuff up. One way to do that is to think abstractly about dessert. For more than 75 years, he and other researchers trying to formalize fairness have been asking the deceptively simple question: What methods for cutting a cake guarantee that everyone who shows up to the party is happy with what they get?
The answers reach far beyond birthday parties. Cake-cutting contemplation is part of a sprawling mathematical subfield focused on the fair division of resources. It has spurred a raft of algorithms informing how to allocate food among hungry communities, how to split rent or chores among roommates, how to draw boundaries for fair voting districts and more. A mathematical problem at its heart, cake cutting connects rigorous reasoning to questions of human preferences and real-world issues, and so attracts not only mathematicians, but also computer scientists, economists, social scientists and legal experts. Questions of fairness (and unfairness) are decidedly universal. Of course, so is dessert. “It’s this very elegant model in which you can really distill what fairness is, and reason about it,” Procaccia says.
The cake, says Steven Brams, a game theorist and political scientist at New York University, is a metaphor for any divisible good, like land or time or limited resources. When cake-cutting insights are applied to settling international disputes, he says, “we are potentially helping the world find solutions.”
Experts have come up with cake-cutting algorithms — the mathematical rules for describing how to cut a cake fairly — many times and in many guises. (The approaches almost always focus on rectangular cakes. The related but more recent “pie-cutting” problem addresses circular desserts or pizza.) The easiest rules reveal how to fairly share a cake between two people: One person cuts the cake into two pieces that they believe to be equal in value, and the other person picks first. Each eater receives a piece that they feel is at least as valuable as the other’s, if not better. Reports of this fair division strategy date back to ancient Greece.
You can argue that fairness, or the lack thereof, is one of the most important problems in the world today.
Steven Brams
In the 1940s, mathematicians began taking serious interest in a mathematical approach to fairness, using cake cutting as an access point. They started exploring how to fairly share among three people, since I-cut-you-choose is a two-player game. That led to looking for ways to extend those algorithms to arbitrarily large numbers of people, and to asking more nuanced questions, like what is fairness exactly, and how do you prove it?
Cake cutting is easy to formulate and easy to relate to, says game theorist Bettina Klaus of the University of Lausanne in Switzerland, who studies fairness in real-world situations like school choice allocation and equal access to housing. “But at the same time, the problem is mathematically interesting and challenging because of its complexity once the number of agents to share the cake grows.”
Recent years have brought progress in identifying the fewest number of cuts needed for a given number of people, as well as the maximum number of cuts, which can get ridiculously high but at least shows that cake cutting is finite. And new variations on the question keep emerging. What if you divide a cake for multiple groups of people instead of individuals? Or, as explored in a paper published last year, what if cake eaters lie about their preferences? And what if you’re divvying up something that comes in discrete, indivisible pieces, like unopened Halloween candies, instead? By focusing on precise definitions and new scenarios, mathematicians have found new applications and kept cake cutting at the forefront of investigations into fairness.
“You can argue that fairness, or the lack thereof, is one of the most important problems in the world today,” says Brams, who over four decades has published hundreds of works on cake cutting or fairness more generally. “And we’re looking at the theoretical foundations of fairness.”
Recipes for fair cake cutting
Documented experiments in finding fair ways to split stuff up go way back, at least to Hesiod’s poem Theogony, written some 2,700 years ago. In one story in the poem, gods and mortals clashed in Mecone, a mythical Greek city. As a sacrifice to appease the gods, Prometheus, who was both a god and humankind’s greatest benefactor, divided a recently slaughtered ox into two piles, one containing unappealing bare bones covered with a layer of fat and the other containing the desirable meat concealed beneath an unappealing section of stomach. Prometheus invited Zeus to take his pick. Zeus, seduced by the shiny fat, chose the unappetizing bones.
In this ancient story, Prometheus infuses the classic I-cut-you-choose strategy — the simplest version of cake cutting — with deception. But when I-cut-you-choose is executed in pursuit of fairness, it should guarantee the satisfaction of everyone involved.
The outcome is proportional, meaning that each player feels like their slice represents a fair share of the total. So for two players, a player would value their own slice at 1/2; for three, a fair share would be 1/3. (And for some arbitrary n number of cake eaters, a fair share would be 1/n.) If the cake is the same throughout, proportionality is equivalent to all the slices being the same size.
How to share cake between two people
You probably already know how to fairly share cake between two people. It’s the simplest approach to fairly cutting cake and is often called the “divider-chooser” method.
-
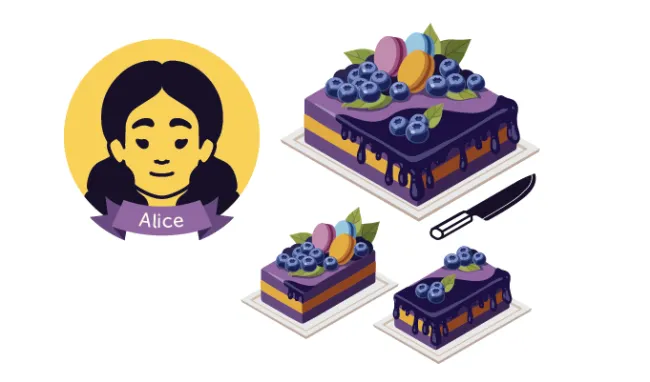
First, one person, in this case Alice, cuts the cake into what she thinks are two fair slices. OLENA SHMAHALO -

The second person, Bob, chooses his preferred slice. Alice gets the remaining slice. Alice is happy because she liked both pieces equally; Bob is happy because he chose his favorite piece. OLENA SHMAHALO
But cake cutting isn’t an interesting mathematical problem if the cake is all the same. Ordinary division and a kitchen scale could readily separate a slab of uniform chocolate sponge into any number of proportional pieces. The problem becomes more complicated if you assume that the cake is heterogeneous — if it’s unevenly frosted, for example, or includes sections of varying flavors and toppings.
A maraschino cherry–lover might choose the smallest slice and feel satisfied if they get the cake’s only cherry. In this case, what mathematicians call the “serendipity of disagreement” gives rise to rich math. The most interesting math arises when there are differing opinions.
A two-person I-cut-you-choose scenario still works here. The divider divides the cake into two pieces of equal value in their view and will be happy with either; the chooser chooses their preferred piece. But increase the number of cake eaters, each with particular preferences, and there’s no easy solution.
Hugo Steinhaus of the University of Warsaw was one of the first mathematicians to dive into this complexity. During World War II, as questions of fair division of land were playing out on a large and violent scale, Steinhaus developed a modified I-cut-you-choose strategy for three players. It came to be called the lone-divider method.
In this approach, one person, let’s call her Alice, cuts the cake into three pieces that she values equally (each at 1/3 of the total). Then a second person, Bob, indicates which of the pieces would be acceptable to him. If he approves at least two pieces, then the third person, Carla, can take any piece she wants, followed by Bob (who has at least one acceptable piece available). Alice gets the one that’s left.
But if either Bob or Carla disapprove of the same piece, then that piece goes to Alice (who valued all pieces equally). The remaining two pieces (which Bob and Carla must value at 2/3 or more of the total) are recombined and shared between Bob and Carla using I-cut-you-choose.
Steinhaus described this algorithm in a short paper published in 1948 in Econometrica. It represented one of the first rigorous investigations in the field of cake cutting. “The rule for the first partner,” Steinhaus wrote, “allows him to cut the object — it may be a cake — as he pleases.”
Steinhaus’ method worked for only three eaters, but in the same paper, he reported that two colleagues had developed an algorithm that could achieve proportionality for any number of cake eaters. The method is known as the last-diminisher method, and it goes like this: One person cuts off a piece of cake they deem to represent a fair share and passes that piece along to the next person. Each remaining player has a chance to either trim the cake (if they think it represents more than a proportional share) or pass (if they think it’s proportionally fair or less than fair). Once everyone has had a chance to trim, or “diminish” the slice, the last person who trimmed gets the piece and exits the game.
The trim is then recombined with the remaining cake, and the process begins again with the remaining players. When only two players are left, they use I-cut-you-choose.
How the “last-diminisher” method works
Sharing cake among three people is harder. In the “last-diminisher” method, three people — Alice, Bob and Carla — each believe they are getting a piece that they value at 1/3 of the total. Mathematicians call that “proportionality,” but whoever exits the game first could still be envious of someone else’s piece.
-

In round 1, the first person, in this case Alice, cuts a piece that she thinks represents 1/3 the value of the cake and passes it to the second person, Bob. OLENA SHMAHALO -

Bob and the third person, Carla, each have a chance to trim the piece, if they think it is worth more than 1/3 the value, or pass. In this case, Bob passes and Carla trims. OLENA SHMAHALO -

The piece goes to whoever trimmed it last — in this case Carla. If both Bob and Carla had passed, Alice takes the piece. OLENA SHMAHALO -

In round 2, any trimmings are added back to the remaining cake, and then the “divider-chooser” method for two people is used. Alice cuts the cake into what she thinks are two fair slices. OLENA SHMAHALO -

Bob chooses his preferred slice. Alice gets the remaining slice. Everyone appears to be happy with their piece. But Carla, who exited the game early, could still think that Alice’s or Bob’s piece is better than hers. OLENA SHMAHALO
Brams has called the last-diminisher method an elegant solution, and it guarantees that everyone judges their own piece to be at least as valuable as a fair share. But it’s not perfect because it doesn’t take envy into account. In both the lone-divider and last-diminisher approaches, a person who exits the game early may end up coveting a piece that is cut later in the game — even though they thought their piece was proportional. These algorithms are not what mathematicians call “envy-free,” which is another way to think about fairness.
There is another practical limitation to the last-diminisher method: With enough players, the cake that remains in later rounds might end up broken apart by a lot of slicing — or even reduced to crumbs. It’s easy to see how a partygoer might not value that as highly as a whole piece.
Can cake cutting be free of envy?
Since the debut of the last-diminisher method, cake cutting has fueled a small but mighty body of serious mathematics.
The 1960s brought a major step forward when mathematicians John Conway and John Selfridge, independently of each other, came up with a new cutting algorithm for three people. Unlike the work by Steinhaus and colleagues, the new recipe achieved both perceived proportionality and avoided any envy among the recipients.
An envy-free solution, in which no one covets another person’s piece, is easy to achieve, points out computer scientist Haris Aziz of the University of New South Wales in Sydney. Just throw the entire cake away. “If you don’t give anything to anybody, that’s envy-free,” he says.
But if the cake lands in the rubbish bin, no one is happy. In Conway’s and Selfridge’s more pleasing scheme, Alice first divides the cake into three pieces she believes are of equal value. Then, Bob can trim one piece — at most — to create a two-way tie for the most valuable. (The trimmings are set aside.) Carla is left to choose among the three. Then the order reverses, and if Carla didn’t choose the trimmed piece, Bob takes it. Alice gets the one that remains. The eaters then turn to the trimmings, following a similar iterative protocol of cutting, trimming and choosing.
How to divide cake with no envy
In a version of cake cutting for three people, each person — Alice, Bob and Carla — are guaranteed to feel that their piece represents 1/3 the total value of the cake. The method, named for John Selfridge and John Conway, also ensures that none of the cake eaters will be envious of another person’s piece. The Selfridge-Conway procedure has been extended for any number people, but the cutting can last a very long time.
-

In round 1, the first person, Alice, cuts the cake into three pieces that she considers equal. OLENA SHMAHALO -
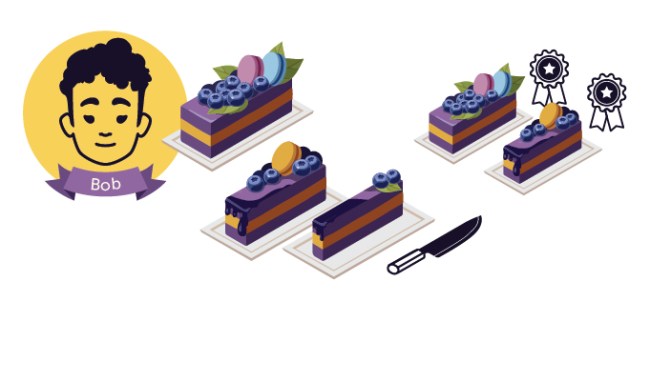
The second person, Bob, can either pass or trim one — and only one — of the pieces to make two pieces that are tied for the best. The trimmings are set aside. OLENA SHMAHALO -
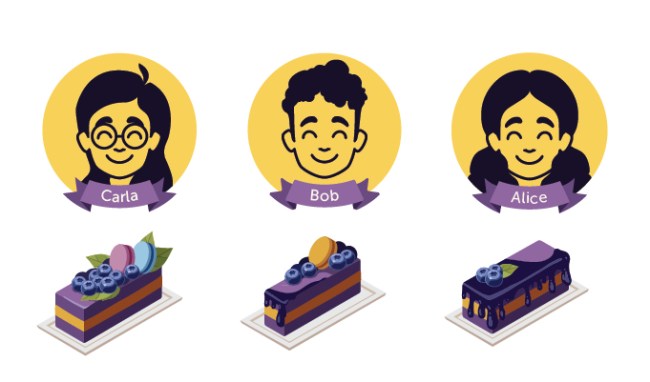
The third person, Carla, gets to pick first — getting her favorite piece. Bob goes next (taking the trimmed piece if Carla doesn’t, thus ensuring he gets one piece that he thought was tied for the best). Alice gets the remaining piece, one of her original pieces. OLENA SHMAHALO -

In round 2, the trimmings are divided. Whoever between Bob and Carla got the untrimmed piece (in this case Carla) cuts the trim into three equally valuable pieces. OLENA SHMAHALO -
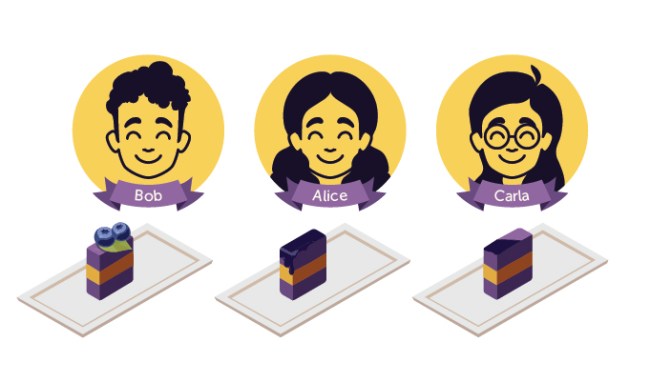
Bob chooses first, getting his favorite piece. Alice, who thought her piece was preferable to the trimmed piece in the previous round, goes next. Carla ends up with one of the pieces she trimmed. This approach is free of envy because Bob got to pick first, Carla valued all the trims equally and Alice feels like any trim is a bonus, since she would have been happy with her original piece alone. OLENA SHMAHALO
Yet for decades more, an envy-free cake-cutting solution for any arbitrary number of eaters remained elusive. In the late 1980s, on his PBS television show For All Practical Purposes: Introduction to Contemporary Mathematics, mathematician Sol Garfunkel featured the unsolved cake-cutting problem and related questions of fair division.
But the problem wouldn’t go unsolved for much longer. In 1995, Brams at NYU and Alan D. Taylor of Union College in Schenectady, N.Y., devised a new procedure that cuts cake for four people with no one envying anyone else. “That was considered a breakthrough of sorts,” Brams says. It built on the “trimming” approach of Conway and Selfridge, running a similar procedure on all possible pairs of cake eaters. Brams and Taylor described how the procedure could be extended to any number of people.
The approach still had limitations. There was no guarantee of how many cuts it might take. “We showed in general that you could require three cuts or 3 million cuts,” Brams says. Or many, many more.
A few years later, mathematicians Jack Robertson and William Webb of Washington State University in Pullman described a useful computation model that could be used to analyze how many steps, including cuts and evaluations, are required by an algorithm. Its calculations confirmed, for example, that no maximum number of cuts could be predicted for any algorithm known at that time that divided cake proportionally and without envy for any arbitrary number of players.
Over the next few decades, many mathematicians came to wonder whether an upper bound for envy-free cake cutting even existed. If not, in theory, cake cutting could go on forever. What’s more, Procaccia says, no one had figured out the minimum, either.
What mathematicians call the “serendipity of disagreement” gives rise to rich math.
Is cake cutting infinite?
Procaccia never actually set out to study cake cutting. In 2008, he was teaching a course on the mathematical foundations of artificial intelligence. One day, walking home after delivering a lecture on resource allocation and the Robertson-Webb model, he realized how he could find a lower bound — a minimum number of steps, including cuts — for envy-free cake cutting for any number of people. The lower bound he found was somewhere around n² steps, where n is the number of cake eaters.
That would lead to his first paper on cake. Procaccia has a knack for giving mathematical papers catchy titles. The lower-bound paper, published in 2009, was titled “Thou shalt covet thy neighbor’s cake.” In 2010, he coauthored one called “Truth, justice, and cake cutting,” which introduced the question of truthfulness — in addition to guaranteeing proportionality and removing envy. If a person hides their preferences during the cutting, someone may end up with an unequal share. It’s “mathematically fascinating,” Procaccia says.
As Procaccia continued in the field, he began thinking more about useful algorithms that could put insights from cake cutting — and the theory of fair division in general — to good use. One example: dividing rent.
The easiest way, of course, is to divide the total due by the number of inhabitants. But that ignores the “serendipity of disagreement.” One person might want a window, another might prefer the bigger closet. In 2014, Procaccia and colleagues designed a web-based tool called Spliddit that collected users’ preferences and produced mathematically fair ways to divide anything, from rent among roommates to possessions among divorcees.
The biggest recent breakthrough in cake cutting, Procaccia says, came from Aziz and computer scientist Simon Mackenzie, based in Sydney, who determined an upper bound on envy-free, proportional cake cutting. First, in 2015, the pair tackled the problem of how to share cake among four people. By borrowing ideas from Conway and Selfridge and from Brams and Taylor, the team devised an algorithm that produced an upper bound of 203 steps, which could include almost as many cuts. That’s a lot but not too unreasonable.
A year later, the team extended the approach to an arbitrary number of people, reporting an algorithm with a finite number of cuts for envy-free, proportional cake cutting. It was a potentially astronomical number of cuts, but it was finite — answering a long-standing question in the field.
Cake cutting for n people, Aziz and Mackenzie reported, could require as many as n^n^n^n^n^n operations. That’s a totally unreasonable number. The maximum number of steps for five people would be around 2 x 102,180. That means five people cutting the cake billions of times per second for 100 trillion years might barely be getting started.
However, Aziz says the algorithm can be adapted to a more reasonable, though still really big upper bound if the partygoers, for example, allow for a little cake to be left over. And it’s still possible that mathematicians could bring that upper bound lower in the future.

The cake-cutting problem asks: What methods for cutting a cake guarantee that everyone is happy with what they get?
MADELINE MCMAHONThe cake-cutting problem endures
Explorations into the question of how to fairly cut a cake aren’t over. Inspired by Procaccia’s 2010 paper on truthfulness, computer scientist Biaoshuai Tao of Shanghai Jiao Tong University investigated what happens when you try to account for dishonest cake eaters. “If everyone knows how the cake is allocated, then I should get more if I tell the truth,” he says.
But in some cases, dishonesty can yield an advantage. If Alice and Bob were to divide a cake, and Alice knew that Bob always preferred chocolate, she might knowingly divide the cake unequally so the smaller piece contained more chocolate. Then Bob would choose according to his preference, and Alice would get the larger piece.
In his work, presented in July 2022 at the Association for Computing Machinery Conference on Economics and Computation, in Boulder, Colo., Tao found that truthfulness and proportionality are incompatible, making it impossible to construct a cake-cutting algorithm that strictly guarantees truthfulness, proportionality and no envy.
Practical applications for cake cutting also continue to abound. Klaus, in Lausanne, points to school choice as an example.
A district with limited seats in certain schools has to balance the school board priorities — scores on entrance exams or geographic distribution, for example — with the preferences of parents to try to find a proportional solution with a fair value. “In the past, schools were just assigned … without asking people what they want,” Klaus says. “The school choice comes from the fact that the preferences of the parents or the kids would be taken into account.”
Over time, cake cutting has evolved into a kind of mathematical sandbox, a constructive playground that brings together abstract proofs and intuitive applications.
And there are plenty of other real-world applications for questions of fair division. Brams has used ideas from cake cutting to study fair voting procedures. (To elect their leaders, at least four scientific societies, including the Mathematical Association of America, adopted an algorithm developed by him.)
Procaccia has applied fair division algorithms to model food allocation. Aziz is exploring applications ranging from how to divvy up chores or other tasks that can’t be divided to how to best schedule doctors’ shifts in hospitals.
Others are studying fair allocation of goods that can’t be cleanly divided. After a divorce, for instance, former partners might come to agreement on a fair split only if some items are taken out of consideration. These investigations include approaches that are close to envy-free if not mathematically perfect.
Even after decades of investigation, cake cutting isn’t like a simple jigsaw puzzle with a well-defined solution. Instead, over time, it has evolved into a kind of mathematical sandbox, a constructive playground that brings together abstract proofs and intuitive applications. The more researchers explore it, the more there is to explore.
“I’m interested in it now not only because it’s beautiful in math,” Tao says, “but I still believe there’s a lot to be done.”






