Circle Game

The geometric realm of circles seems an unlikely setting for a startling mathematical discovery. A staple of geometry textbooks, the circle is already the subject of myriad theorems and countless exercises.

Nonetheless, researchers motivated by curiosity about a striking pattern of smaller circles packed within a larger circle have now found an extraordinary new formula that mathematicians had previously overlooked. The formula, which has to do with the curvatures of touching circles, has also yielded elegant generalizations that encompass spheres and analogs of circles in higher dimensions.

“No one had noticed it before,” says statistician Allan R. Wilks of AT&T Laboratories in Florham Park, N.J., who initiated the research. “It’s amazing to find something new in something so old and so classical.”

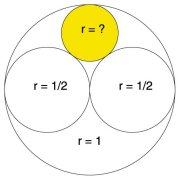
The route to the discovery began with a high school geometry problem. In 1998, during a lull in a conference in Germany, Wilks started talking with a colleague who was pondering his daughter’s homework assignment. The question concerned a pattern made up of two identical circles that fit side by side inside a third circle. The assignment was to find the radius of a fourth circle nestled between the outer circle and the two inner circles.

After Wilks had returned to the United States, he found the three-circle pattern still on his mind. In drawing it, he could easily insert smaller circles into the empty spaces among the larger circles. Each new circle would be as large as possible without overlapping the circles already present.

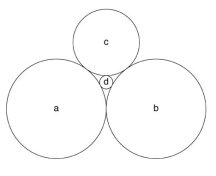
Wilks wondered about the relative sizes of the touching circles. He found his answer in a geometry textbook. In 1643, French mathematician René Descartes had developed a formula relating the curvatures of four circles that all touch, or are tangent to, each other.

He defined the curvature of a circle as the reciprocal of its radius. Hence, if the radius of a circle is one-fifth (1/5) that of another, its curvature is 5 times that of the larger circle.

Given four mutually tangent circles with curvatures a, b, c, and d, the Descartes circle equation specifies that (a² + b² + c² + d²) = 1/2 (a + b + c + d)².

Negative curvatures

The same formula holds for three touching circles nested within a fourth circle, which is the configuration that Wilks was examining. In this case, however, the curvature of the outer circle would be a negative number, because the other circles touch it from the inside rather than the outside. The formula also applies to configurations in which one or two of the touching circles are replaced by straight lines. A line counts as a circle with zero curvature.

Using the Descartes circle equation, Wilks could readily calculate the curvature and radius of each new circle he placed in his drawing. For example, if the initial, outer circle has a radius of 1, its curvature relative to circles inside it would be –1. Two smaller circles of the same size drawn inside the initial circle would each have a radius of 1/2 and, hence, a curvature of 2. The next largest circles that would fit snugly in the remaining space between circles would each have a radius of 1/3 and a curvature of 3.

Once an initial configuration of four circles is set, the Descartes circle equation specifies the size of every smaller circle that fits into the pattern. Moreover, if the curvatures of the four initial circles are integers, the curvature of every smaller circle is also an integer.

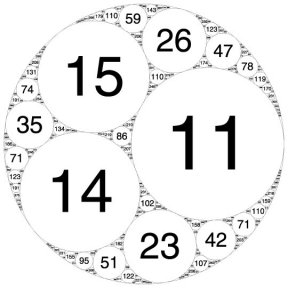
Wilks decided to use a computer to plot a large diagram of the circle pattern, labeling each circle with its curvature. “It makes a pleasing picture,” Wilks says. “It’s symmetric, and the numbers get bigger as the circles get smaller.”

For convenience, he decided to put the origin of his plot at the center of the outer circle and to orient the x axis so that it passes through the centers of the two inner circles. It was a fortuitous choice. When Wilks checked the coordinates of the centers of the circles he was plotting, he noticed that the pairs were all rational numbers (fractions). To his surprise, he found that multiplying each coordinate of a circle’s center by the circle’s curvature always produced an integer. In other words, if a circle has curvature b and its center at point (x, y), bx and by are integers.

Intrigued by the result, Wilks showed his work to his coworker Colin L. Mallows, also a statistician at AT&T Labs. Mallows came up with a mathematical proof of the relationship that Wilks had found. He then generalized the result to produce a formula that relates the curvatures and coordinates of the centers of four mutually tangent circles—just as Descartes had done for curvatures alone.

There had been no clue at all that such a formula should exist. “It was completely unexpected,” says mathematician Ronald L. Graham of the University of California, San Diego.

The new formula looks like the original Descartes equation for four mutually tangent circles, provided the coordinates of the centers are expressed as so-called complex numbers.

A complex number has two parts and can be written as a + bi, where a is the “real” part and bi is called the “imaginary” part, with i representing the square root of –1. These numbers can be plotted as points on a graph. Each complex number has a “real” x coordinate and an “imaginary” y coordinate. For example, the complex number 3 + 4i would be plotted as the point (3, 4) on what mathematicians term the complex plane.

The existence of this relationship among the centers of tangent circles allows anyone to derive a relation that makes it very easy to plot exquisitely detailed tangent-circle patterns on the computer. Wilks generated a huge plot that he put on display on the wall outside his office.

With its great intricacy and cryptic spirals of numbers, the posted design attracted a great deal of attention. One of those who fell under the pattern’s spell was Jeffrey C. Lagarias, a mathematician at AT&T Labs.

Lagarias recognized the pattern as an

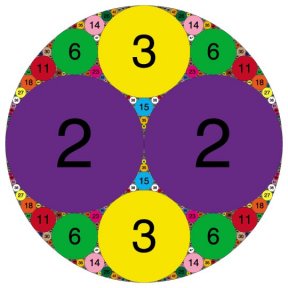
example of an Apollonian packing—a type of arrangement named after a Greek mathematician who studied tangent circles more than 2,000 years ago. Such an arrangement is created by repeatedly filling the spaces between touching circles with smaller touching circles. In Wilks’ case, the Apollonian packing was made up of circles with integer curvatures.

Such circle packings can be described by the curvatures of the first four circles that go into the pattern. The example that Wilks generated, for example, has the label (–1, 2, 2, 3). “There are infinitely many such packings,” Lagarias notes.

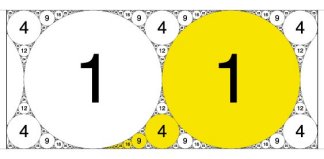
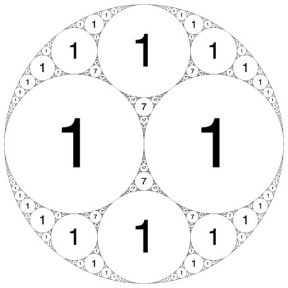
Although some patterns are highly symmetric, others have no symmetry at all. For example, the Apollonian circle packing (0, 0, 1, 1) features neatly ordered circles tightly packed between a pair of parallel lines. On the other hand, the packing labeled (–6, 11, 14, 15) is nonsymmetrical.

Lagarias, Mallows, and Wilks went on to generalize the formula, which they now call the new Descartes circle theorem, to cover configurations made up of the higher-dimensional analogs of touching circles, beginning with touching spheres in three-dimensional space. They also developed a way to represent Apollonian packings in both spherical and hyperbolic geometry (SN: 12/23&30/00, p. 408), which involve curved rather than flat surfaces.

To imagine these two realms, consider a triangle. If you draw any triangle on a flat sheet of paper and add up its three angles, the result is always 180 degrees. When you draw a triangle on the surface of a sphere, however, the angles invariably add up to more than 180 degrees—a characteristic of spherical geometry. In hyperbolic geometry, represented in two dimensions by a saddle-shaped surface, the angles of a triangle add up to less than 180 degrees.

Number patterns

The three researchers developed mathematical expressions to represent and plot what they describe as hyperbolic and spherical Apollonian packings. Although the patterns still look like those generated on a flat sheet of paper, the numbers giving the curvatures of the constituent circles are strikingly different.

When Graham saw the huge poster of an Apollonian circle packing outside Wilks’ office, he was fascinated by the curvature numbers in the pattern. “Where do these numbers come from?” he asks. “What’s going on here?”

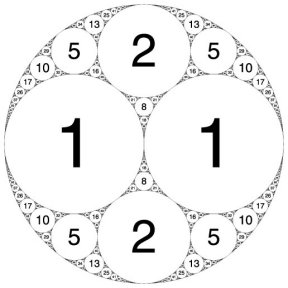
One familiar pattern shows up in the (0, 0, 1, 1) packing, which nests circles between two parallel lines. The two largest circles have a curvature of 1. The next largest circle that rests on a line and nestles between the two largest ones has a curvature of 4. Zooming in on the gap between circles reveals a circle of curvature 9. In general, the curvatures of the successively smaller circles crowded into the original gap form a sequence of perfect squares: 1, 4, 9, 16, 25, 36, and so on.

The sequences of numbers are more mysterious in other parts of this packing and in other packings. “You get a lot of numbers you can’t explain,” Graham says. The patterns are often not obvious, and the mathematical origin of the patterns can be difficult to ascertain.

Graham, Lagarias, Wilks, and their coworkers have studied a large number of different packings to look for clues about why and how often certain integers appear in various packings, and why some integers don’t appear at all. The effort has involved a tremendous amount of computation, because it includes minuscule circles having curvatures in the hundreds of thousands.

Any given area of an Apollonian packing, no matter how tiny, contains circles. “There are so many circles, every [sufficiently large curvature] should be hit lots and lots of times,” Lagarias says. If certain curvatures are missing, then something strange must be going on.

Insights and proofs, however, are hard to come by. “These are very challenging problems in number theory,” Graham says. “When you dig in, it gets hairier and hairier.”

With different people bringing different perspectives to the same mathematical structures, Apollonian circle packings have quickly developed into a rich, promising field of study. Lagarias described some of the results at the Joint Mathematics Meetings held earlier this year in New Orleans. Wilks and his collaborators have also submitted for publication several papers about the new Descartes circle theorem.

This is all curiosity-driven research with no foreseeable application in mind, Lagarias observes. “It involved starting with a picture and seeing a pattern, then trying to understand where it comes from.”