Grab a pen and draw a figure. Follow a few rules: keep your lines straight, don’t pick up your pen, don’t cross the lines, and finish at the spot where you started. You’ll have a polygon.
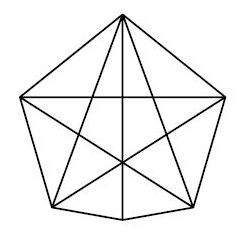
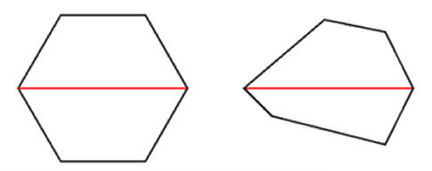
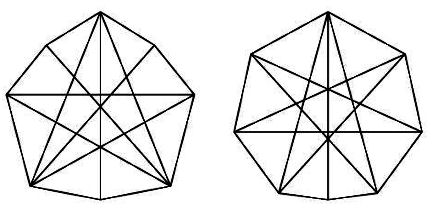
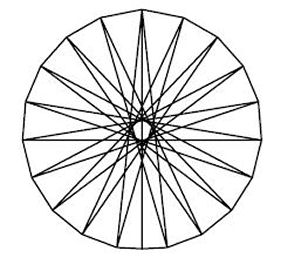
Polygons are among the simplest mathematical objects in existence. Even so, they hold mysteries. Here’s one: What is the polygon with the largest area that has n sides and fixed diameter?
Mathematicians still don’t know. Michael Mossinghoff of Davidson (N.C.) College has made some recent advances on the question, however. In January, he presented them at the 2007 Joint Mathematics Meetings in New Orleans. Mathematicians had already tackled the problem for some types of polygons, but Mossinghoff broke new ground for polygons with an even number of sides numbering 10 or more.
Stick with four sides, and the polygon problem has a fairly simple answer. Squares are the largest four-sided polygon with a given diameter, although certain oddly-shaped quadrilaterals have an equally large area.
Mathematicians have also solved the problem for polygons with an odd numbers of sides. In each case, the regular polygon, with equal angles and equal sides, is the winner.
But for polygons that have an even number of sides and more than four sides, the results are peculiar. Mathematicians don’t know the answer for most even numbered polygons, but they do know that the regular polygon loses every time.
That’s a rather bizarre fact, given that changing the problem slightly can make the regular polygon win every time. If you use a fixed perimeter, rather than a fixed diameter, the regular polygon is always the largest polygon, no matter how many sides it has. But it turns out that fixing the diameter—the greatest distance across the polygon—generates a fascinating playground for mathematicians. There is no easy way to find the biggest polygon with a given diameter.
Mathematicians have solved the problem for a couple of even-sided polygons with fixed diameter, which they call “isodiametric polygons.” In 1975, Ronald Graham of AT&T Bell Labs (now at the University of California, San Diego) figured out that the largest isodiametric six-sided polygon looks a bit like a regular pentagon with one side pushed out a bit. Its area is about 3.92% larger than the regular hexagon. Graham speculated that all of the largest isodiametric polygons would have a roughly similar shape.
In 2002, a group of mathematicians cracked the eight-sided case. As Graham had conjectured, the largest one looks a bit like a regular 7-gon with one side pushed out a bit. It has 2.79% more space than a regular octagon.
No one knows the biggest isodiametric polygon for a figure with 10 or more sides, but Mossinghoff has broken some ground. Instead of searching for the single biggest isodiametric polygon with a particular number of sides, he just hunted for an isodiametric polygon with a larger area than the regular polygon. Although his goal may seem relatively modest, it actually very ambitious: rather than tackling only the 10 or 12-sided polygon, he wanted to find a way to generate an n-sided polygon larger than the regular n-sided polygon for any even-numbered n greater than 8.
Following Graham’s lead, Mossinghoff started by considering the regular (n–1)-gon and pushing one side out a bit. This was already larger than the regular n-gon, but Mossinghoff wanted to find even larger shapes. He wrote down equations for a polygon’s area in terms of the angles formed by the diameters connecting its vertices.
He then used numerical optimization software to find solutions to his equations that would generate large polygons. He found polygons that were bigger than the regular polygon and bigger than his first approach for any even number of sides greater than four. Although Mossinghoff’s polygons are larger than any others found so far, he doesn’t know whether even larger ones exist.
Now he’s pursuing a related query: Which equilateral polygon has the greatest perimeter? He may never run out of unsolved polygon questions.
If you would like to comment on this article, please see the blog version.






