The study of prime numbers has long been a central part of number theory, a field traditionally pursued for its own sake and for the mathematical beauty of its results. The number theorist Don Zagier once commented that “upon looking at prime numbers, one has the feeling of being in the presence of one of the inexplicable secrets of creation.”
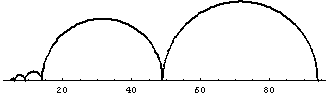
A prime is a whole number (other than 1) that is evenly divisible by itself and 1. This simple definition leads to the following sequence of numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, and so on.
Prime numbers are the building blocks of integers. Positive integers other than primes, known as composite numbers, can be written as the product of smaller primes. In fact, according to the fundamental theorem of arithmetic, any composite number can be represented in exactly one way as a product of primes.
Over the centuries, mathematicians have invented a variety of tools for probing the structure of integers, as they search for patterns and relationships among primes and composites. Recently, a novel mathematical function called the number derivative has come into play.
Here are the rules, as applied to primes, p, and composite numbers, nm:
- The number derivative of a prime, p‘, is 1.
- The number derivative of a composite number, (nm)’, is n‘m + m‘n.
- The number derivative of 1, or 1′, is 0.
Because the second rule looks like the so-called product rule in calculus, the term “derivative” has become associated with this function.
The number derivative “provides a different context from which to view many topics of number theory, especially those concerning prime numbers,” says Linda Westrick. “The complex patterns which arise from its simple definition make it interesting and worthy of study.”
A high school senior at Maggie L. Walker Governor’s School in Richmond, Va., Westrick placed fourth in this year’s Intel Science Talent Search with a project that involved a detailed study of the intriguing properties of the number derivative.
Suppose you want to take the number derivative of 6. According to the number derivative rules, 6′ = (2 x 3)’ = 2′ x 3 + 2 x 3′ = 1 x 3 + 2 x 1 = 5. You can then take the number derivative of the answer, 5, to get 1. So, the second derivative of 6 (or 6″) is 1. The third derivative of 6 (or 6″‘) is 0.
The following table lists the first, second, and third number derivatives of the first 18 positive integers.
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
n‘ |
0 |
1 |
1 |
4 |
1 |
5 |
1 |
12 |
6 |
7 |
1 |
16 |
1 |
9 |
8 |
32 |
1 |
21 |
n“ |
0 |
0 |
0 |
4 |
0 |
1 |
0 |
16 |
5 |
1 |
0 |
32 |
0 |
6 |
12 |
80 |
0 |
10 |
n“‘ |
0 |
0 |
0 |
4 |
0 |
0 |
0 |
32 |
1 |
0 |
0 |
80 |
0 |
5 |
16 |
176 |
0 |
7 |
To facilitate her search for patterns, Westrick developed her own way of visualizing what happens when you take successive derivatives of a given integer.
For example, the successive number derivatives of 94 are 49, 14, 9, 6, 5, 1, and 0. The jumps from one number to the next can be visualized as arcs of circles along a number line (below).
Depending on the starting integer, successive number derivatives can behave in surprising ways. The derivatives of 99 increase without bound, for example. In other cases, the values change erratically, going up or down at various points.
The study of the number derivative has proved to be remarkably rich. “Many unsolved problems of number theory can be posed in the context of the number derivative,” Westrick says.
For example, is it true that for each positive integer b, there exists an integer n such that n‘ = 2b? Because the number derivative of the product of two primes is the sum of those primes, a proof of Goldbach’s conjecture would also prove the truth of this statement, Westrick says.
Goldbach’s conjecture posits that every even number larger than 2 is the sum of two prime numbers.
Westrick went on to formulate the number derivative for rational numbers of the form a/b. She then extended the function to the negative rationals. Westrick also looked at characteristics of solutions to the “differential” equation x‘ = a.
There are many surprising and beautiful patterns, Westrick says.
Westrick first came across the number derivative when she attended the Research Science Institute last summer at the Massachusetts Institute of Technology. Her adviser, Pavlo Pylyavskyy, had seen it defined in a problem posed at the 14th Summer Conference of International Tournament of Towns, organized by the Moscow Academy of Science in 2002.
For many months, Westrick thought that she had the field of research on the number derivative all to herself. But she wasn’t quite alone. Last year, Victor Ufnarovski and Bo Åhlander of Sweden published a paper in the Journal of Integer Sequences on “how to differentiate a number,” covering some of the topics that Westrick had also pursued.
When Westrick recently found out about and read the paper, she was intrigued by the areas of overlap and by the alternative approaches to various topics. Westrick herself was invited to present her findings at an international mathematics conference last month in Bulgaria.
“I love working on difficult math,” Westrick says. “For hard problems, I make lists and draw pictures and look for patterns that I believe are there, and I find the work worthwhile even when I don’t make tangible progress.”
“Whether I’m proving theorems, designing robots, or inventing new math, my goal is the same: to create something beautiful,” she adds. “I hope to add to the beauty and simplicity of existing theories and create beautiful math of my own. I hope to inspire others by what I create.”






