A typical daisy is a star-like flower. It features a fringe of white or colored petals and a central disk of tubular florets. Each floret is itself a tiny flower.



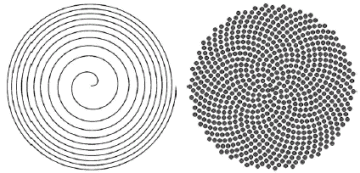



The tightly packed florets at a daisy’s center have an intriguing arrangement. The florets get larger at greater distances from the center. And there are hints of clockwise and anticlockwise spirals in the pattern.
One way to model such a pattern is to start with a curve called Fermat’s spiral. This curve is also known as a parabolic spiral. It’s given by the polar equation
r = k a1/2
where r is the distance from the origin, k is a constant that determines how tightly wound the spiral is, and a is the polar angle.
This type of spiral has the property of enclosing equal areas with every turn.
By placing points (disks or polygons) centered at regular angular intervals along such a spiral, you can create a variety of intriguing patterns—depending on the angle you choose to use. Using the angle 222.49 degrees (a value related to the golden ratio, 1.618034. . . ), you get a pattern with an even packing of polygons (or disks). It closely resembles a daisy’s florets.
By choosing other angles, you get intriguing variants. Each choice gives a different pattern of secondary spirals, some winding clockwise and others anticlockwise, which form an interlocking system. Robert Dixon explores some of these possibilities in his book Mathographics.
Using larger numbers of points and smaller angles produces patterns with a variety of secondary spirals and, often, with radial lines that become evident toward the edges. Michael Naylor of Western Washington University has investigated a variety of such patterns (see “Golden Blossoms, Pi Flowers” at Golden Blossoms, Pi Flowers).
Robert J. Krawczyk of the Illinois Institute of Technology in Chicago has taken the generation of these patterns another step further, creating striking images of eerie ripple patterns. He calls these circular designs “Fermat’s spiral mandalas.”
Krawczyk starts by combining several spirals to create one complex pattern.
By placing points at fixed angular intervals along these curves, he gets very elaborate patterns that show a variety of features.
To finish his images, Krawczyk enhances the texture and gives them a coppery glow. Examples of such mandalas can be seen at http://home.netcom.com/~bitart/.
A mandala’s complex circular design, with its symmetrical and radial balance, is intended to draw the eye to its center, Krawczyk says. Fermat’s spiral, in particular, “is a natural basis for this inward draw.”
For those who prefer a more natural look, all it takes is a close-up view of a daisy’s central disk.






