Symmetry attracts us. Studies comparing people’s reactions to different faces have shown, for example, that they find highly symmetrical faces more attractive than less symmetrical faces. The symmetry of faces is simple and bilateral, but other three-dimensional objects can be symmetric in complex ways, leading to different kinds of beauty.






Bathsheba Grossman, a sculptor in Santa Cruz, California, mines subtle forms of symmetry for inspiration. Her results are swirling and proportional. They may be simple or complex, but they always come together into a precise, intriguingly symmetrical pattern.
When Grossman dreams up a new sculpture, she starts by contemplating what its symmetries will be. In mathematical terms, she thinks about its symmetry group. “I have to pick a group before I can come up with an idea,” she says.
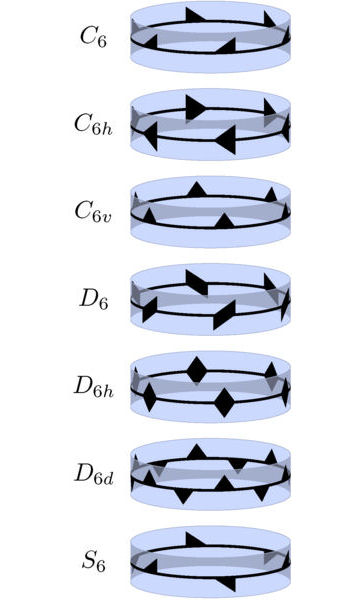
Three-dimensional objects can be symmetrical in a variety of ways. Mathematicians have identified all of the different symmetry groups that such objects can have. The two most basic kinds of symmetry are “reflective” and “rotational.”
In the mathematical sense, an object has rotational symmetry if there is an axis around which you can spin it so that at the end of a less-than-complete rotation, it looks just the same as it did at the beginning.
An object has reflective symmetry if there is a plane across which you can invert it without changing its appearance. For example, a face has reflective symmetry across the vertical plane that goes down the center of the nose to the back of the head.
Various combinations of those two basic symmetries form symmetry groups, which are mathematical constructs that show all the different symmetries of a particular object.
Grossman’s favorite form of symmetry is remarkably simple: It contains 180-degree rotations around its three perpendicular coordinate axes. “Three rotations and no reflections; what could be finer?” she muses.
Various combinations of rotations around the coordinate axes and reflections across the coordinate planes produce seven different families of symmetry groups.
Some of Grossman’s sculptures have very few symmetries but are still remarkably complex. Antipot, for example, has 180-degree rotational symmetry around a vertical axis. It has a second symmetry that comes from reflecting it across a horizontal plane while at the same time rotating it 90 degrees. “It’s really hard to get a good picture of something that has this symmetry group,” Grossman says. “It’s very hard to understand it.”
A few years ago, Grossman asked John Conway, a mathematician at Princeton University, if he could think of an object in the real world that has the same symmetry group as Antipot. “The only example he could come up with is a baseball if you consider the stitching to be directed,” Grossman says. “This is a symmetry group that practically nothing in the world has.”
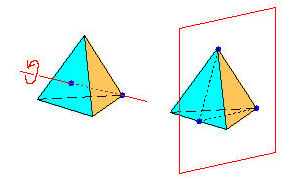
The five regular solids—the cube, tetrahedron, octahedron, dodecahedron, and icosahedron—each have symmetries around axes other than their three perpendicular coordinate axes. The tetrahedron, for example, has 120-degree rotational symmetry around the axes going from any vertex to the opposite face. It also has reflective symmetry across each plane that goes through an edge and across the two opposite faces.
Mathematicians have derived seven symmetry groups from the five regular solids. It might seem like five objects should have five symmetry groups, but some regular solids have more than one symmetry group. For example, some three-dimensional objects share all of the symmetries of a tetrahedron, but some share only the rotational symmetries.
Furthermore, the symmetries of some regular solids are related to the symmetries of others. The symmetries of a dodecahedron (a 12-sided solid), for example, are the same as those of an icosahedron (a 20-sided solid).
The symmetry groups of Soliton, Antipot, and Ora are artistically the three very best groups, according to Grossman, who says, “All but those three are beneath consideration.” The simplicity of those three groups allows for elegant artistic expression, she says, while their multiple axes of symmetry bring out the complexities of three-dimensional space.
Grossman’s designs are so complex that it is nearly impossible to construct them using traditional molding techniques. In the last decade, a technique called three-dimensional printing has become feasible, however. This method is what allows Grossman to construct her sculptures. In fact, it has transformed her work.
Contemplating her sculpture Antichron, Grossman says, “Even though this thing is so simple, I discovered it. No one had seen it before. The reason these things are walled off from human experience is that they’re unmoldable. I wonder how many similar things exist—objects that are very, very simple and elegant, yet never manufactured.”
If you would like to comment on this article, please see the blog version.






