Of the irrational, transcendental numbers, pi seems to get all the attention. Web sites and books celebrate its quirks and quandaries. Its digits have been computed to 1,241,100,000,000 decimal places.
Lagging far behind in the celebrity sweepstakes is the number known as e. Carried to 20 decimal places, e is 2.71828 18284 59045 23536. Only 1,250,000,000 of its decimal digits have been computed so far—though there appears to be an unverified computation of 1.7 billion digits. People can’t even agree on its proper name. It’s been called the logarithmic constant, Napier’s number, Euler’s constant, and the natural logarithmic base.
One way to define e is as the number that the expression (1 + x)1/x approaches as x gets smaller and smaller. Thus, when x is 1, the expression equals 2; when x is .5, the expression is 2.25; when x is .25, the expression is 2.4414. . . , and so on.
You can also obtain an approximate value of e by summing the following terms, where n! represents the product of all integers from 1 to n:
1 + 1/1! + 1/2! + 1/3! + 1/4! + . . . + 1/n!
This expression is sometimes described as Newton’s series approximation for e. It’s also known as the Maclaurin series expansion or the Direct Method.
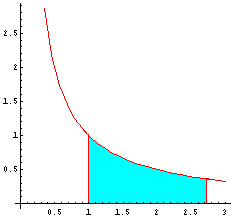
In graphic terms, e is the number (greater than 1) for which the area below the curve y = 1/x, above the x axis, to the right of the line x = 1, and to the left of the line x = e is precisely equal to 1.
The number e comes up in a wide variety of mathematical contexts. The constant also plays a key role in descriptions of phenomena such as radioactive decay and population growth and, in the financial world, in calculations of compound interest.
In 1998, two math buffs, inventor Harlan J. Brothers and meteorologist John A. Knox, discovered new, amazingly simple formulas for calculating e.
Brothers had begun his search for new formulas for e in early 1997. He mailed his first results to the National Public Radio program “Science Friday,” which is based in New York City. At that time, Knox’s wife was an intern at “Science Friday,” and she happened to open the letter that Brothers had sent. A climatologist with a background in mathematics and physics, she passed it on to her husband, who was then at Columbia University and the NASA/Goddard Institute for Space Studies in New York City. Knox, who had been a college math major, confirmed that Brothers had found a novel, correct approach to calculating e.
The two men started collaborating. “Together, using no more mathematical knowledge than is taught in college calculus, we discovered and formally proved more than 2 dozen new algebraic expressions that yield e to extraordinary accuracy,” Knox said at the time. Some of these formulas outperform conventional methods used to approximate e to a large number of decimal places.
Here’s one example. As x gets larger, the expression [(2x + 1)/(2x – 1)]x gets closer and closer to e. For x equal to 10, the expression yields (21/19)10, or 2.72055. . ., which is e accurate to two decimal places. For x equal to 1,000, you get e to 6 decimal places.
“We’ve even used a version of this expression to obtain e correct to 30,000 decimal places,” Knox said. “Not bad for an expression that an eighth-grader could understand, yet one that eluded the founding fathers of calculus and all their successors.”
“What’s more, we have discovered other new expressions for calculating e that are even better,” he added. For example, try out [(2 + 2–x)/(2 – 2–x)]2^x.
Brothers has continued to investigate e‘s quirks. In the January College Mathematics Journal, he presents new series expressions for approximating e. Here’s one example of such a series:
1/0! + 3/2! + 5/4! + 7/6! + 9/8! + 11/10! + 13/12! + 15/14! + . . .,
where each term has the form (2k + 1)/(2k)!, with k starting at 0.
Other series approximations use terms of the following forms: (2k + 2)/(2k + 1)!; (3 – 4k2)/(2k + 1)!, or [(3k)2 + 1]/(3k)!.
These new series include the fastest known methods for computing e. They converge to the value of e much more quickly than Newton’s original expression, which has long been the basis for computing the value of e.
Brothers describes the so-called compression techniques he used to develop series approximations that improve upon Newton’s original method in his College Mathematics Journal article. “Using techniques familiar to any first-year calculus student, it is indeed possible to derive series that converge more rapidly,” he says.
“It is hoped that the inherent symmetry and numerical beauty of these newly derived expressions might provide inspiration to students, educators, and all who are drawn by the allure of numbers,” Brothers concludes.
“Students should also feel encouraged to explore other well-known series, such as those associated with pi, to examine which of them might lend themselves to effective compression,” he suggests.
In the meantime, the spotlight is on e.
“The logarithmic constant e is famous for turning up whenever natural beauty and mathematical elegance commingle,” Brothers and Knox concluded in an article in the Mathematical Intelligencer describing their 1998 discoveries. “Our work provides a new glimpse of its austere charm.”
The continuing fascination with e may indeed signal an improved, updated image for this venerable, under-appreciated number.
Originally posted: 11/7/98
Updated: 2/14/04






