“Need a zero-volume bottle? Searching for a one-sided surface? Want the ultimate in nonorientability?”



The intriguing subject of these cryptic entreaties is a bizarre mathematical object known as a Klein bottle, discovered in 1882 by German mathematician Felix Klein (1849-1925).
An ordinary bottle has an inside and an outside. To walk from the inside to the outside, a fly would have to cross the lip that forms the bottle’s mouth. A Klein bottle has no such edge. What appears to be its inside is continuous with its outside.
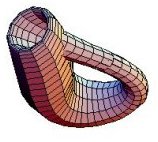
One way to describe a Klein bottle is in terms of instructions for making one from a rectangular sheet of paper. Glue together the two horizontal sides, and glue together the vertical sides after twisting one side 180 degrees. By itself, the first instruction produces a cylindrical tube. The second instruction by itself produces a Möbius strip, a remarkable mathematical surface that has only one side and one edge (see Möbius and His Band, July 8, 2000).
Combining the two instructions presents a delicate problem. To bring the cylinder’s two ends together in their proper orientations, one end has to curl around and plunge through the surface, then meet the other end from the inside. In other words, the surface has to intersect itself.
If one were to make a model of a Klein bottle out of glass, there would have to be a circular hole where the stretched-out, bent end intersects the tube’s side. In a true Klein bottle, there is no hole. There’s only an intersection of the surfaces. That technical difficulty, however, hasn’t stopped glassblowers from taking up the challenge of fashioning glass models of these strange objects.
Astronomer Cliff Stoll of Oakland, Calif., first heard of Klein bottles in the 1960s. After reading about them in an article by Martin Gardner in Scientific American, he went to his high school chemistry lab, set up a bunsen burner, and tried his hand at making one. “After burning my fingers and cracking a dozen tubes, I gave up,” he recalls.
Three years later while in college, Stoll tried again, this time with gloves and better equipment. Same problem. “Without enough heat, you can’t bend the glass. Heat it too much and the glass melts into a glob. And at the right temperature, it’s practically impossible to stretch glass around a curve and down inside itself,” he says. “So I gave up a second time.”
After surviving graduate school and three postdocs, Stoll ended up in Berkeley. One day, a glassblower asked him to help program an oven temperature controller. Stoll spent a few hours on the project, then asked the glassblower some questions about what it would take to make a glass Klein bottle. A week later, thanks to the efforts of glassblowers Tom Adams and Paul Chittenden, who specialize in making intricate, scientific glassware, Stoll finally had his Klein bottle.
“My first Klein bottle was made from a Pyrex 500-milliliter Erlenmeyer flask, with welded glass connections,” Stoll reports. He showed it to a math professor, who insisted on buying it.
“So I made another,” Stoll says. “Another mathematician asked for it. So I made a few more, and they walked away. I thought, ‘Why not make a bunch and try to sell ’em?’ So I worked with the glassblowers and made a few dozen. I sold them within two months.”
So began Stoll’s boutique business: Acme Klein Bottles. Stoll calls it the world’s only zero-volume enterprise.
“These elegant bottles make great gifts, fantastic classroom displays, and inferior mousetraps,” Stoll notes on his Klein bottle Web site. “With its circle of singularities, an Acme Klein Bottle can be said to exist inside of itself-especially handy during time reversals.”






