It’s a Rough World

In the realm of mathematics, perfection abounds. Lines stretch straight to infinity, planes are flawlessly flat, and spheres are impeccably round. The real world, however, is almost always irregular–the jagged spear of a lightning bolt, the rough face of a broken rock, and the ragged profile of a mountain range are just a few examples. Although people have always been surrounded by texture, until recently they could not describe it in anything other than qualitative terms such as smooth or rugged or lumpy. Long after scientists developed ways to measure physical properties such as temperature, weight, and time, the techniques needed to quantify roughness eluded them.

Then came fractals.

Before these mathematical tools were developed during the 1960s, scientists usually represented the physical world using only three dimensions. Lines occupy one dimension; planes, two; and cubes, three.

But fractals freed scientists from the tyranny of integer dimensions and enabled them to describe objects using fractional dimensions.

Not only do such representations of objects show roughness and irregularity, they do so across the entire range of scale. A close-up look at a jagged nonfractal line would reveal that its made up of small, straight segments. But for a fractal line–say, a 1.3-dimensional line–the view would be the same from afar as from close-up. Each segment would have the same degree of roughness no matter the scale at which its viewed. Likewise, a microscopic look at a rock with a 2.7-dimensional surface would display the same texture as the telescopic view of a cliff face with the same fractional dimension.

Far from being merely mathematical abstractions, fractals pop up throughout the natural and the humanmade world. They appear in the swirling patterns on a flowing liquids surface (SN: 1/23/93, p. 53) and the patchy mosaics of urban sprawl (SN: 1/6/96, p. 8).

Scientists have used fractals to analyze all sorts of irregular objects or phenomena, from swings in the stock market to the frequency of natural disasters, says Donald L. Turcotte, a geophysicist at Cornell University. One of the first uses of fractals in geosciences was a simple one, describing the roughness of Britains coastline. Today, researchers are applying fractals to far-ranging topics–the probability of wildfire, as well as the spread of toxic fluids through rocks and soil.

Natural disasters

Earthquakes, wildfires, and other large-scale phenomena are the focus of many fractal analyses. The relationship between the frequency and the magnitude of earthquakes is fractal, Turcotte notes. When researchers plot these two quantities on a logarithmic graph, the data points fall on a line. In such a correspondence between the two quantities, called a power-law relationship, the slope of that line is an exponential power that can be employed as a fractal dimension. Fractal equations allow scientists to more easily develop computer models to simulate how often earthquakes occur.

Scientists first noted the power-law relationship between the frequency and magnitude of earthquakes in the 1950s–well before fractals were invented, says Bruce D. Malamud, a mathematician at Kings College in London. The relation holds for earthquakes of almost all sizes.

More recently, Malamud and his colleagues showed that a power-law relationship exists between the frequency and size of wildfires. The researchers discovered that the fractal relationship held true for four different sets of wildfire data, even though the sets were compiled for areas of the world radically different in terrain and vegetation. Malamud says that the consistent relationship between the size and the frequency of wildfires–even for time periods as short as 2 years–gives hazard-management personnel an opportunity to use limited amounts of data to predict the likelihood of wildfires of various sizes in an area.

Scientists are now subdividing the four wildfire data sets to see if intervention–either extinguishing fires before they die out naturally or setting preventative fires to remove dried brush–changes the relationship between the size and frequency of blazes. The new analyses could reveal whether certain firefighting policies affect the location and intensity of wildfires in unexpected ways, Malamud says.

Fractal fractures

Many phenomena related to the fracture of rocks and minerals, from tiny bits of volcanic ash to the large blocks of Earths crust that scrape past each other during earthquakes, can be described or modeled using fractals. North of Los Angeles, the two sides of the San Gabriel Fault sandwich a 6-meter-thick layer of pulverized material. This crushed rock, called gouge, can be found between the surfaces of many faults, says Charles G. Sammis, a geophysicist at the University of Southern California in Los Angeles.

The power-law relationship between the number and the size of the particles, from large rocks to fine mineral grit, has a fractal dimension of 1.6, Sammis notes. In other words, chunks of rock with a cross-sectional area of 1.6 units are about one-tenth as common as those with a cross-sectional area of 1 unit.

This fractal relationship holds across a wide range of particle sizes, he adds.

Gouge forms in the early life of a fault, says Sammis. Stress transfers from one side of the fault to the other through bridges of large rocks. When the stress along the fault is high enough to break the gouge particles, it fractures only those that are bearing the load. As the load shifts to new bridges, those rocks fracture, and the debris is gradually ground into finer and finer grains, all the while maintaining a size distribution with a fractal dimension of 1.6.

Computer models that simulate particles of rock trapped in a moving fault, as well as laboratory tests with pellets of crushed granite, also generate a distribution of particle sizes with a fractal dimension of 1.6. This specific value is interesting, Sammis explains, because it seems to mark a transition point for the behavior of faults. For values more or less than 1.6, the gouge does not transfer stress across the fault because bridges dont form. In those cases, the two faces of the fault slide past one another without triggering an earthquake. When the value equals 1.6, however, the rock bridges lock the fault and stress builds up until a temblor occurs.

Many other characteristics of fractured rock are fractals, notes Christopher C. Barton, a geophysicist with the U.S. Geological Survey in St. Petersburg, Fla. For example, the relation between the number and the lengths of fractures in many types of rock follow a fractal, power-law relationship on scales that range from long fissures in Earths crust down to microscopic cracks in small stones.

Flowing through the rock

Scientists have developed computer models that use fractals to simulate the movement of fluids through permeable rock, such as limestone. Rina Schumer, a hydrologist at the Desert Research Institute in Reno, Nev., and her colleagues model the spread of fluid through fractured and porous rock. A rocks porosity–the percentage of the materials volume thats occupied by space between solid grains–can easily be expressed as a fractal dimension.

By taking just a few measurements of rock and soil characteristics near the site of a toxic spill such as a fuel leak, for example, researchers can use fractals to estimate the directions and speeds at which the fluid will travel through the surrounding earth. This information can be useful to emergency-response personnel, and it may eventually help government officials develop plans to protect aquifers from spills.

Models that use fractals to simulate the presence of fractures in porous rock may provide better answers than those that assume the rock is uncracked. For example, Department of Energy scientists modeling the potential seepage of fluids from Nevadas Yucca Mountain Project–an underground repository being designed to hold radioactive waste from nuclear plants (SN: 1/19/02, p. 39: Official chooses Nevada for nuclear waste)–estimate that if a leak were to occur, it would take about 1,000 years for the first traces of tainted fluid to reach 5 kilometers from the site. However, that analysis assumes that waste simply seeps through unfractured rock, says David T. Purvance, a hydrogeologist at hydrOhm Environmental Geophysics in Reno.

A fractal analysis that incorporates the effect of fractures in the rock predicts a much faster travel of liquid radioactive waste. A model that uses a previously measured distribution of crack sizes in the regions so-called fractured welded tuff–a cracked, porous rock made up of volcanic ash particles that have been fused together under extreme heat and high pressure–estimates that spilled waste could travel a distance of 5 km in only 200 years.

Volcanic dimensions

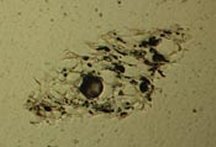
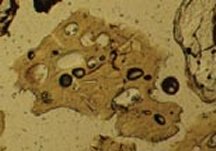
Although the roughness of the glassy particles spewed out by volcanic activity doesnt keep the same fractal dimension across all scales, measuring that parameter of the ash bits nevertheless may help scientists analyze the pattern of a volcanos past eruptions. Anton H. Maria and Stephen N. Carey, both volcanologists at the University of Rhode Island in Narragansett, studied ash ejected from five different eruptions, including some deep undersea.

The researchers found that the combination of fractal dimensions of the ash particles measured at two different scales enabled them to discriminate among the eruptions. The surface roughness of the ash on the larger scale was linked to the abundance of large bubbles in the molten rock that had erupted from the volcano. The explosive power of the eruption shattered the rock along these bubbles, leaving small particles with ragged edges. At smaller scales, the ash particles roughness was linked to the abundance of small bubbles trapped within the material as it cooled. These two factors explained more than 90 percent of the differences among the ash particles from the five eruptions, says Maria.

The size of the bubbles in the volcanic ash particles seems to be influenced by several factors, including the type and amount of gases that accompanied the eruption and whether the eruption was explosive or relatively calm. Ash particles from eruptions on land, where the ash cloud spewed directly into the air, typically have different fractal dimensions from those produced by underwater volcanic activity.

These distinctions are particularly important because they may help scientists track a volcanos long-term history in areas where there are few if any written records, says Maria. By analyzing particles from different ash layers in a long sequence of eruptions, researchers might be able to tell whether all of a volcanos eruptions have been explosive or its strong eruptions were interspersed with calmer belchings of ash.

---