When you learned to tie knots as a child, you probably thought their main use was for making bows on birthday presents or keeping your shoes on your feet. However, if a small band of mathematicians and physicists has its way, knots will form the basis for an entirely new kind of computer, one whose power vastly outstrips that of the machines at our disposal today.

In its first century, the mathematical study of knots belonged squarely to the realm of pure mathematics, seemingly divorced from any practical applications. In the past decade, however, mathematicians have turned knot theory into a bridge between two seemingly unconnected subjects: computer science and quantum mechanics, the branch of physics that deals with the ultrasmall scale of atoms and subatomic particles.
In a paper published last month, researchers propose that this connection between the two fields might finally enable physicists to reach a decades-long goal: to exploit quantum physics to build a computer whose performance would far surpass that of computers based on the classical physics of Isaac Newton. A quantum computer, if it is ever built, will have the power to crack the cryptographic schemes that safeguard Internet transactions and to create incredibly detailed simulations of the behavior of the universe at the tiniest scale.
The knots that mathematicians have been studying have a slight quirk: After the theoretical knot is tied, the ends of the string are joined together so the knot can’t untie. The same knot can appear in many guises, since pulling and twisting the strings can make the knot look completely different. The basic question of knot theory is, Given two knots that look very different, is there a way tell whether they are knotted in the same way (SN: 12/8/01, p. 360: Available to subscribers at Knot Possible)?
To distinguish between knots, mathematicians look for numerical characteristics of a knot, such as the number of times the knot’s shadow crosses itself. Some other characteristics, called knot invariants, don’t change when the knot is pulled and twisted about. If two knots have different invariants, they must be different knots.
At the heart of the connection between computer science and quantum physics is a knot invariant called the Jones polynomial, which associates a given knot with an array of numbers. The Jones polynomial involves a complex mathematical formula, and although calculating it is easy for simple knots, it is enormously difficult for messy, tangled knots. In fact, mathematicians have found compelling evidence suggesting that as knots get more and more complicated, the difficulty of computing their Jones polynomials rises exponentially. Calculating the Jones polynomial for complicated knots is considered beyond the reach of even the fastest computers.
That seems like bad news. A connection to quantum physics, however, has turned this apparent liability into a decided advantage by offering a new approach. In the late 1980s, physicist Edward Witten, a major figure in string theory (SN: 2/27/93, p. 136), described a physical system that should calculate information about the Jones polynomial during the course of its regularly scheduled activities–just as when a ball is hurled into the air, nature instantly solves the complicated equations that govern its motion.
Now, mathematician Michael Freedman of Microsoft Research in Redmond, Wash., and physicist Alexei Kitaev of the California Institute of Technology in Pasadena are pursuing a daring idea: If Witten’s physical system somehow does calculations beyond the reach of computers, could this system be harnessed to build a completely new kind of computer?
Nature as computer
The idea of a physical system calculating something about knots or other loops may sound strange, but in fact examples of such systems abound, even in basic physics. In an electrical transformer, for instance, two loops of wire are coiled around an iron core. An electric current passing through one of the wires generates a voltage in the other wire that’s proportional to the number of times the second wire twists around the core. Thus, even if you couldn’t see the wire, you could figure out its number of twists simply by measuring the voltage. Witten proposed that in the same way, it should be possible to obtain information about the Jones polynomial of a knot by taking appropriate measurements in a more complicated physical system.
The connections between the Jones polynomial and both computers and quantum physics caught Freedman’s eye in the late 1980s. Freedman was on his home turf when it came to knots–in 1986, he was awarded a Fields Medal (the mathematical equivalent of the Nobel prize) for his work in topology, the mathematical field to which knot theory belongs. However, he knew less about the challenges of building an actual physical system like Witten’s theoretical system. Physicists “said Witten’s physics was so abstract it wasn’t related to the real world, and that we’d never be able to build such a computer in our universe,” Freedman recalls. Discouraged, he put the project on the back burner.
As Freedman gradually learned more physics, however, he became convinced that certain extremely cold electron seas called quantum Hall fluids might offer the right physics to do the job. Then in 1997, working independently, Kitaev described a concrete model for how such a computer might work. “Kitaev’s paper was stunningly original,” says John Preskill, who studies quantum computation at the California Institute of Technology in Pasadena. “It’s a beautiful and potentially quite significant idea.”
In the past several years, Freedman and Kitaev have joined forces to explore the promise of their model for what they call a topological quantum computer. Such a computer would encode information not in the conventional zeros and ones but in the configurations of different braids, which are similar to knots but consist of several different threads intertwined around each other. The computer would physically weave braids in space-time, and then according to Witten’s theory, nature would take over the hard work, carrying out complex Jones polynomial calculations in the blink of an eye.
Polynomial power
A computer specially geared to calculate the value of some obscure knot invariant might not seem particularly useful. However, in the late 1980s, mathematicians showed that computing the Jones polynomial belongs to the famous family of what they call NP-hard problems. If someone could find a fast way to calculate the Jones polynomial, the numerical output of the calculation could then be used to solve a host of other difficult problems. These include the traveling salesman problem, which looks for the most efficient route for a salesman who must pass through many cities.
“There’s an impressive amount of information stored in the Jones polynomial,” Freedman says.
Kitaev and Freedman’s model computer wouldn’t provide the exact value of the Jones polynomial, only indicate whether its value lies within a certain range. However, even that is enough to solve many important problems. Last year, Freedman and Kitaev, together with mathematicians Zhenghan Wang and Michael Larsen of Indiana University in Bloomington, proved that a topological quantum computer would be every bit as effective as another theoretical quantum computer, the “qubit” quantum computer, which employs quantum physics but uses it in a very different way (SN: 2/1/03, p. 77: Available to subscribers at Quantum computers to keep an eye on).
Both types of computers are expected to have the power to crack cryptographic schemes, such as the RSA algorithm commonly used in Internet security, including credit card transactions. “A lot of people belonging to agencies with three letters in their name will be very interested if someone is able to build these computers,” says Seth Lloyd, who studies quantum computation at the Massachusetts Institute of Technology.
Although researchers have been thinking about how to build qubit quantum computers for decades, so far they languish on the drawing board. The main difficulty is that in a qubit computer, each bit of information is typically encoded in the state of a single particle, such as an electron or photon. This makes the information vulnerable: If a tiny disturbance in the environment changes the state of the particle, the information is lost forever. Physicists call this problem decoherence. “Decoherence is the number one enemy of quantum computation,” Preskill says.
By encoding information in braids instead of single particles, a topological quantum computer neatly sidesteps this problem. A small disruption from the environment might disturb the threads of a knot slightly but is extremely unlikely to change its overall knottedness– just as a breeze might make your shoelaces flutter but not untie. Thus, the topological quantum computer has a built-in defense against decoherence. “I think it’s the right way to go in the long run, if you want to build a quantum computer,” Preskill says. “It’s a made-to-order solution to the problem of decoherence and errors.”
Topological quantum computation’s stability might eventually give it the edge over qubit computers, Lloyd says. “Topological quantum computation is far away from realization now, but it has such appealing features that it wouldn’t take me by surprise if it turned into the dominant paradigm,” he says. “It’s such an elegant idea to use what nature gives you to build quantum computers that are intrinsically reliable.”
Computation, anyon?
For building a topological quantum computer, one system that Freedman and Kitaev are considering is an exotic form of matter called a fractional quantum Hall fluid. It arises when electrons at the flat interface of two semiconductors are subjected to a powerful magnetic field and cooled to temperatures close to absolute zero. The electrons on the flat surface form a disorganized liquid sea of electrons, and if some extra electrons are then added, strange quasi-particles called anyons emerge. Unlike electrons, which each have a single negative charge, or protons, which have a single positive charge, anyons can have a charge that is a fraction of a whole number–something never before seen in physics.
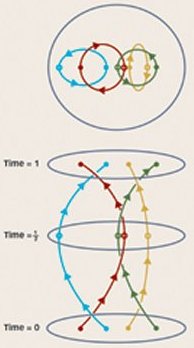
Anyons have a strange property that may make them the key to topological quantum computation. If you slide a bunch of pennies around on a table along paths that return the pennies to their original spots at the end, then after the motion is over there is no way to tell what paths the pennies followed (unless you have a very dusty table). When anyons are moved around each other, however, they remember–in a specific physical sense–the knottedness of the paths they followed.
Imagine several anyons on a surface, and suppose they move around along complicated paths, ending up where they started. On the surface, the paths may cross each other in many spots. However, in space-time–in which there is one snapshot of the surface for each moment in time–the paths don’t pass directly through each other, but simply braid around each other.
Anyons come in a variety of types, and if two different anyons bump into each other, they either annihilate each other or fuse into a single particle. When anyons move around each other along braided paths, the motion changes the pattern of the anyons’ interactions with each other–a change physicists call a unitary transformation. This transformation alters what will happen if two anyons collide, so by bumping anyons into each other it’s possible to tell that they have moved.
What’s more, different braids lead to different transformations, so one can figure out something about the particular braid the anyons traversed by measuring what happens when the anyons collide. The fractional quantum Hall fluid has effectively calculated numerical properties of the braid, and measuring the anyons gives information about the result of this calculation.
Quantum Hall fluids come in many flavors, depending on the fractional charge of the anyons. Different fluids have different unitary transformations and so carry out different calculations. If the transformations in a particular fluid aren’t very complicated, then the corresponding calculations aren’t very interesting. So, the task now is to find an anyonic system with complex enough transformations–called nonabelian transformations–to carry out Jones polynomial calculations. So far, the few quantum Hall systems that have been studied thoroughly aren’t powerful enough to do the job, but Freedman is optimistic that the right systems exist. “Nonabelian anyons are not obscure mathematically–they’re rather simple, and there’s no overriding physical law that has to be broken to make them,” he says. “I feel confident that they’re out there, but there’s no way of knowing right now whether they’ll be easy or hard to put together.”
Although quantum Hall fluids are the only known systems that contain anyons, many other anyonic systems probably await discovery, suggests physicist Chetan Nayak of the University of California, Los Angeles. “With quantum Hall fluids, we stumbled by experiment into a new category of matter, and we’ve just scratched the surface in terms of new possibilities,” Nayak says. He has teamed up with Freedman to explore the possibility of creating nonabelian anyons in systems consisting of many thin layers of magnets. Kitaev, meanwhile, is investigating the possibility of building memory for a quantum computer from a system in which electrons spinning on the corners of a hexagonal grid give rise to anyons.
Freedman is reluctant to put a time frame on the construction of a topological quantum computer, but he is confident that it will happen. “If the physical world is the way we think it is, it’s only a matter of time,” he says.
If a quantum computer is built, its uses will go far beyond cracking cryptographic schemes. A quantum computer could simulate the interactions of individual molecules and atoms, rapidly carrying out enormous computations that today’s computers do agonizingly slowly. It’s hard to guess ahead of time just how engineers and physicists will employ such a vast increase in computing capacity, says Daniel Gottesman, who studies quantum computation at the Perimeter Institute in Waterloo, Ontario. “When classical computers were invented, no one imagined that engineers would someday use them to test the design of airplanes or bridges,” he says.
With engineers turning their attention to designing single-molecule drugs, robots, and machines, it would be useful to have a quantum computer to probe matter on this tiny scale, Gottesman says.
For Freedman, though, there’s a motivation even more compelling than the possibility of creating a powerful new computer. “I’m working on this because the mathematics is so beautiful,” he says. “It’s an excuse to think about the two most interesting things in the world: topology and theoretical physics.”
****************
If you have a comment on this article that you would like considered for publication in Science News, please send it to editors@sciencenews.org.
To subscribe to Science News (print), go to https://www.kable.com/pub/scnw/
subServices.asp.
To sign up for the free weekly e-LETTER from Science News, go to http://www.sciencenews.org/subscribe_form.asp.






