Polyhedron Man

A towering stack of 642 compact disks could represent an impressive music or software collection. The same number of CDs strung together into iridescent arcs can be a mathematical sculpture.

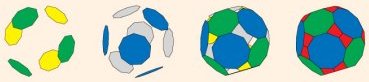
Such a glittering assemblage, more than 6 feet in diameter, hangs in an atrium of the computer science building at the University of California, Berkeley. Titled “Rainbow Bits,” the sculpture slowly rotates in response to air currents. Viewers experience a kaleidoscope of fleeting glints, dazzling colors, and shifting shadows.

Created by George W. Hart of Northport, N.Y., the sculpture is more than an intriguing visual effect. Its strands of recycled CDs trace the edges of a novel mathematical solid–a polyhedron made up of 20 equilateral triangles and 60 kite-shaped quadrilaterals.

This particular solid, which Hart dubs a propellorized icosahedron, is one example of a newly defined class of polyhedra. “As far as I know, these forms have never previously been described by mathematicians,” Hart says.

Hart’s Berkeley sculpture is just one of his many creations based on polyhedra. Hart has

also collaborated with mathematicians and computer scientists to define and visualize a variety of new mathematical shapes.

“As a sculptor of constructive geometric forms, I try to create engaging works that are enriched by an underlying geometrical depth,” Hart says. “I share with many artists the idea that a pure form is a worthy object.”

Such forms tantalize artists and scientists alike. “George Hart is a very special individual, a gifted mathematician, a creative artist, and an inspiring teacher,” says Berkeley computer scientist Carlo H. Séquin. “He is among the very best of a rather small group of people who successfully integrate art and mathematics. Hart’s geometrical constructions are intriguing, educational, and artistic at the same time.”

Passion for polyhedra

The sculptor’s passion for polyhedra was already evident by the time he had reached his teen years. He enjoyed making large structures, including mathematical solids, by painstakingly gluing together hundreds upon hundreds of toothpicks. Inspired by a book about mathematical models, he later took to constructing intricate polyhedra out of paper.

Hart majored in mathematics, then earned graduate degrees in linguistics and in electrical engineering and computer science. He taught computer and engineering courses at Columbia University and Hofstra University in Hempstead, N.Y. Along the way, he wrote a textbook on multidimensional analysis, a branch of mathematics that relates physical measurements to one another. He also developed and patented methods for determining the energy consumption of individual appliances from measurements of total power used by a household.

Hart is currently a visiting scholar with the computational geometry group at the applied mathematics and statistics department of the State University of New York at Stony Brook. He devotes the bulk of his time, however, to his varied polyhedral pursuits.

“Polyhedra have an enormous aesthetic appeal,” Hart contends. Moreover, “the subject is fun and easy to learn on one’s own,” he notes.

Since 1996, Hart has been building a remarkable Web site devoted to all things polyhedral (http://www.georgehart.com). Its enormous catalog of polyhedra now includes many solids never previously illustrated in any publication.

Hart’s Web pages “provide important information for my university courses on geometric modeling,” Séquin says. Furthermore, he adds, “they provide inspiration for me as a part-time artist, and they provide sheer visual pleasure for geometrically inclined minds.”

Linking polygons

Polyhedra are made by linking triangles, squares, hexagons, and other polygons to form closed, three-dimensional objects. Different rules for linking various polygons generate different types of polyhedra.

The Platonic solids, known to the ancient Greeks, consist entirely of identical regular polygons, which are defined as having equal sides and equal angles. There are precisely five such objects: the tetrahedron (made up of four equilateral triangles), cube (six squares), octahedron (eight equilateral triangles), dodecahedron (12 regular pentagons), and icosahedron (20 equilateral triangles).

If you relax the conditions for generating the Platonic solids and specify that faces must be regular but not necessarily identical polygons, there are 13 such polyhedra, known as Archimedean solids. One example is the truncated icosahedron, familiar as the pattern on a soccer ball, which consists of 12 pentagons and 20 hexagons.

Polyhedra also can be constructed from polygons that don’t necessarily have equal sides and equal angles, and they may be indented or spiky, like three-dimensional stars. The great stellated dodecahedron, first described by 17th-century mathematician Johannes Kepler, is one example of a spiky polyhedron. Nonindented polyhedra, such as the Platonic solids, are called convex.

Hart has delved deeply into the history of the discovery and representation of polyhedra. During the Renaissance, he notes by way of example, Leonardo da Vinci invented a way to show the front and back of a polyhedron without confusion by depicting edges as if they were made from wooden laths and leaving the polyhedron’s faces open.

Inspired by Leonardo’s drawings of wooden models, Hart has crafted his own beautiful models of these designs. He has also programmed computers that guide stereolithography machines to produce, layer by layer, three-dimensional plastic replicas of the models.

With a vast palette of geometric solids to choose from, Hart has fashioned polyhedral models and sculptures from all sorts of materials and objects, including Plexiglas, brass, papier-mché, pipe cleaners, pencils, floppy disks, toothbrushes, paper clips, and plastic cutlery.

He “brings the ideal forms of the polyhedra into the material world with wit and humor,” says computer programmer and artist Bob Brill of Ann Arbor, Mich. “The austere beauty of the polyhedra is thus made accessible and familiar.”

New possibilities

Given the lengthy history associated with polyhedra, it may seem astonishing that there are still mathematical discoveries to be made. Hart has proved particularly adept at identifying rules and variants that lead to new possibilities.

For example, his discovery of propellorized polyhedra came out of a new notation for describing polyhedra, proposed by mathematician John H. Conway of Princeton University. In Conway’s scheme, a capital letter specifies a “seed” polyhedron. For example, the Platonic solids are denoted T, C, O, D, and I. A lower-case letter then specifies an operation. The combination tC means truncate a cube; that is, cut off the corners of a cube to form a new solid with six octagonal and eight triangular faces. Conway’s simple notation can be used to derive the Archimedean solids and infinitely many other symmetric polyhedra.

In the course of writing a computer program to implement Conway’s notation, Hart tried to think of a simple operator that wasn’t yet included in Conway’s list. He came up with what he called the propellor [sic] operation: Start with a polyhedron, then spread apart the faces and introduce quadrilaterals so that each face is surrounded by a ring of these forms.

“The [propellor] operation can be applied to any convex polyhedron and combined with other operations to produce a variety of new forms,” Hart says. “These provide a storehouse of intriguing structures, some of which have inspired artworks.”

Hart based his design for “Rainbow Bits” on an icosahedron transformed via his propellor operator into a three-dimensional mosaic of 20 equilateral triangles and 60 kite-shaped quadrilaterals. The resulting sculpture required one CD at each vertex, five CDs along each of the longer edges, and three CDs along each of the shorter edges. The positions and angles of slots cut into the CDs determined their placement.

“For many visitors, this stunning sculpture is a main attraction of our building, particularly when it is hit by rays of sunlight and [sprays] intense colored spots over the atrium walls,” Séquin says.

Generating novel forms

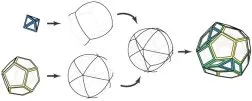
Working with Craig S. Kaplan of the University of Washington in Seattle, Hart has recently invented a procedure for generating many polyhedral forms, including new types of polyhedra. Dubbed symmetrohedra, these geometric solids result from the symmetric placement of regular polygons (see illustration below).

The new technique generates a variety of known polyhedra, including most of the Archimedean solids, and infinitely many new ones. One particularly striking product is a polyhedron made up of 20 regular nine-sided polygons (called enneagons), 12 regular pentagons, and 60 isosceles triangles. “You rarely see enneagons in a polyhedron,” Hart comments.

In another recent effort, Hart and computer scientist Douglas Zongker of the University of Washington developed a novel method for constructing polyhedra by blending together two or more existing polyhedra.

Hart, Zongker, and Kaplan all described their new visualization methods at a meeting that highlighted mathematical connections in art, music, and science, held last July at Southwestern College in Winfield, Kan.

Beauty and joy

Whether assembling an intricate polyhedral design, leading a model-building workshop, or describing his latest ventures, Hart brings an infectious enthusiasm to his task. To help spread the word about the beauty and joy of polyhedra, he recently coauthored a book on building models using Zome plastic components, produced by Zometool of Denver. Embodying mathematical ratios such as the golden mean, the system’s balls and sticks lend themselves to polyhedron building. On another communications front, Hart is now writing a history of polyhedral geometry in art.

“The best way to learn about polyhedra is to make your own paper models,” Hart insists. For those who prefer to skip the spilled glue, misshapen corners, ill-fitting edges, and hours of work, Hart’s Web site provides interactive, three-dimensional virtual models that can be observed from different perspectives.

Brill says about Hart, “His energy, his curiosity, his inventiveness appear to be boundless.” Those qualities come in handy when exploring the infinite realm of polyhedra.