Normal 0 false false false MicrosoftInternetExplorer4
Jules Mikhael and his colleagues didn’t set out to make a material with a structure that had never been seen before, much less one that combines order and irregularity in a whole new way, one that Archimedes hinted at 2,000 years ago, one bound together by the Fibonacci sequence. They just wanted to understand a quasicrystal.
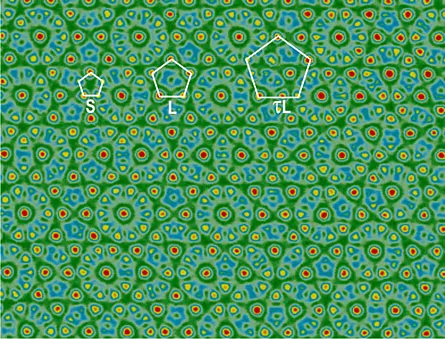


Even that wasn’t such a modest goal, because quasicrystals are pretty odd critters. Slice one in half, and there is a sort of mosaic with repeating shapes like tiles, much like a crystal. But here’s the bizarre part: Spin the resulting mosaic a fifth of a turn and often its tiles will line up exactly as they were before you spun it.
But that kind of five-fold symmetry is “forbidden,” because mathematicians have shown that no repeating flat pattern has it. That’s why you’ve never seen a bathroom tiled with regular pentagons—it’d be impossible to cover the whole surface with no gaps.
The secret of a quasicrystal is that its patterns never repeat. The tile shapes within the quasicrystal combine and recombine, with one area perhaps looking similar to another but then skipping off in its own unique formation. This eternal irregularity also gives quasicrystals remarkable, intriguing properties. For example, they tend to be slippery like Teflon, and even when made from metals, they’re good insulators.
Physicists have never really understood why quasicrystals have these properties, though. “This is the one million dollar question,” says Clemens Bechinger, one of the Mikhael’s colleagues at the University of Stuttgart.
Part of the difficulty is that quasicrystals are frustratingly complicated. They’ve generally been made from mixtures of several different metals, and this chemical complexity on top of the inherent structural complexity confuses matters.
To simplify matters, the team set out to create a quasicrystal from micron-sized plastic beads called colloidal particles. This approach would make the chemistry simple. Furthermore, they’d be able to see the quasicrystal structure with a microscope. In metal alloys, the structure is so tiny — on the scale of atoms — that physicists have been stuck inferring the structure from X-ray diffraction techniques.
Colloidal particles are negatively charged, so when poured into a flat pan of water, they naturally form a grid of triangles as they try to get as far as possible from one another. This structure is like a crystal: repeating, perfectly orderly, rather dull.
Then the team switched on five lasers, arranged so that the light beams would interfere with one another and create a complex pattern with lots of five-fold symmetry. The plastic beads were attracted to the spots where the laser was most intense, creating the quasicrystal the team had been hoping for.
Bechinger and Mikhael’s team had accomplished their goal of creating a quasicrystal that would help explain quasicrystal properties, but their most important discovery was still ahead of them. They tried lowering the intensity of the lasers. When the lasers were very low, the beads ignored the lasers entirely and formed a triangular grid. But at an intermediate stage, the beads formed a pattern very close to an Archimedean tiling, one of the repeating patterns that had long been believed to be the only type possible. The beads formed rows of repeating triangles or repeating squares, but the rows didn’t alternate evenly the way they would in an ordinary Archimedean tiling. Like a quasicrystal, they formed an overall pattern that never repeated.
But that isn’t to say that there was no order. The pattern of triangular rows and square rows, the team realized, was derived from another ancient piece of mathematics: the Fibonacci sequence. This is the sequence that begins 1, 1, 2, 3, 5, 8 … , with each subsequent number being the sum of the previous two.
The poor beads, the team deduced, were torn in their loyalties, repelled from one another but also attracted to the intense laser spots. So they had split the difference. The irregular pattern in the vertical direction made the beads line up as close as possible to the quasicrystalline shape the laser beams demanded, while the repeating horizontal patterns aligned them as close as possible to the grid pattern their mutual repulsion pushed them toward.
“We are absolutely sure that this structure should have properties that are not usual,” Mikhael says, because materials with odd structures almost always do. Now they just have to figure out what those properties are.






