Rating the rankings

The single best school in the country is PennState. Then again, maybe it’s Princeton. Or perhaps Johns Hopkins, or Harvard, or Notre Dame …

Each of these schools could legitimately claim to be on top, according to a mathematical analysis, posted recently on ArXiv.org, of the data U.S. News & World Report uses to generate its influential and controversial rankings of American undergraduate institutions. It all depends, the researchers say, on what your priorities are.

The magazine uses seven key factors in its ratings, including things like percentage of alumni who donate, acceptance rates for admission, and spending per student. Lior Pachter of the University of California, Berkeley and Peter Huggins of CarnegieMellonUniversity reasoned that all these factors are probably relevant to the quality of a university, but one student might value a university with a low student-faculty ratio, for example, while another might care more about research funding. Was there a way to analyze the data, they wondered, that wouldn’t rely on an arbitrary selection of priorities?

Techniques they’d developed for a completely different problem — aligning gene sequences to understand evolutionary changes — could be adapted to do just that, they realized. Biologists commonly analyze the differences between the DNA of two closely related creatures in order to understand how they evolved.  Normal 0 To do that, researchers first have to decide how to line the two gene sequences up, identifying the segments that are identical and the places where DNA has have mutated or moved around or been deleted. But this alignment requires some guesswork: How likely, for example, it is that a gene will have mutated, and how likely is it that it simply will have been deleted? Biologists have little basis for deciding that, Pachter says, just as U.S. News has little basis for deciding how important one of its factors is for a particular person.

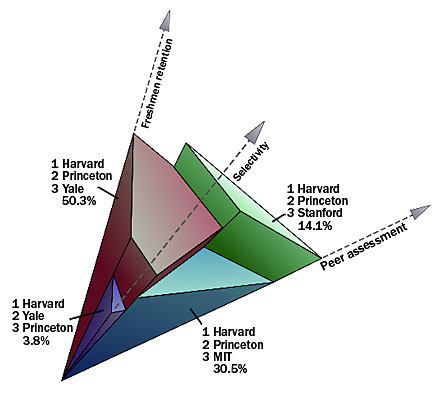
Huggins and Pachter had attacked this biological question using high-dimensional geometry, so they did the same for the educational data. They imagined each university as a point in seven-dimensional space, with one dimension for each factor that U.S. News considers. Although seven-dimensional space is hard to visualize, it’s easy to perform calculations on: Each point is represented by a sequence of seven numbers, just as a point in two dimensions can be represented by a pair of numbers. A university’s scores in the seven factors provide its particular sequence of seven numbers, and the universities thus form a cloud of points in seven-dimensional space. The researchers could then examine the “space” formed by all the universities by looking at the smallest flat-sided object (called a polytope) that contains them.

A particular set of priorities among the seven factors could also be represented in this same geometric space. Each of the seven numbers of the sequence this time would represent the relative importance of each factor. So, for example, a student who cares enormously about the research funding available at a university might consider that factor to be 70 percent of the decision and all the others to each be 5 percent. If research funding were the first factor in the list, that student’s priorities could be represented by the point (70, 5, 5, 5, 5, 5, 5). A student who cared especially about alumni satisfaction, as shown by their donation rates, might have priorities represented by the point (5, 70, 5, 5, 5, 5, 5).

Now imagine an arrow from the origin (the point whose coordinates are all zero) to the point that represents a particular student’s priorities. The researchers found something neat: If you extend that line until it hits the polytope, the university whose point is closest to where the line hits will represent the school that, according to that student’s priorities, is the best.

Finding the second or third best school, according to a particular set of priorities, required a bit more mathematical maneuvering but the same basic technique applied. The researchers then calculated the range of rankings a particular school could have according to all possible sets of priorities, excluding fluke rankings a school achieved only rarely.

The top schools, they found, were top pretty much regardless of one’s priorities. Harvard and Princeton and Yale, for example, were always in the top five, because they were strong across the board on all the criteria.

Schools that were a bit more uneven could vary wildly, though. PennState, for example, was 48 according to the magazine’s criteria, but it could also be as high as 1 or as low as 59. That variability evolves because PennState is the best at making sure students graduate, according to the data from U.S. News, but weaker in other aspects. UC Berkeley, on the other hand, was strong in most categories except for one: alumni giving. (Public schools like UC Berkeley typically have much lower donation rates than private ones.) As a result, although U.S. News rates UC Berkeley as 21, the university could go as high as 14 or as low as 36.

“What we found is that these rankings are kind of arbitrary,” Pachter says. “If you care more about student-faculty ratios than alumni giving, you’re going to get a different ranking. It’s very biased to give only one view.” The pair argue that the magazine should release several different rankings, based on choices of a few representative sets of priorities.

“But that doesn’t sell magazines,” says Kevin Rask, an economist at WakeForestUniversity in Winston-Salem, N.C., who has studied the impact of the U.S. News rankings. “People want to see who’s Number One and who’s Number Two, we want to see who’s going up and who’s going down.” The study shows nicely, he says, how that interest can be at odds with a true evaluation of quality.

One stumbling block Huggins and Pachter had to overcome is that U.S. News is secretive about some of its data. The magazine releases the precise values for the total score for each university and for three of the criteria, but the values of four of the criteria remain secret. So the researchers had to reverse-engineer what the individual scores for the secret criteria were likely to have been for each of the universities.

The pair point out that their methods can’t address another of the fundamental criticisms of the U.S. News evaluations, that the magazine chooses the wrong factors to base their evaluations on in the first place.

These techniques can be applied to any situation that requires ranking according to varying priorities, the researchers say. Similar lists are made, for example, of the best cities to live in, or the best graduate schools. Huggins and Pachter are now applying their methods to voting in elections with more than two candidates.