Sand Drawings and Mirror Curves

To accompany the telling of a story or recounting of a fable, men of the Chokwe people in south-central Africa traditionally made sand drawings, called sona, to illustrate the tale. These highly stylized geometric illustrations also served as memory aids.

The storyteller would clean and smooth the ground, then use his fingertips to press into the sand a rectangular grid of equidistant dots. As he talked, he would trace a winding line among the dots. More often than not, he would draw the line in one continuous motion to create a closed loop. A line could intersect itself but could not be traced over again.

This sand drawing (right) illustrates a fable in which a rabbit, positioned at point B, discovers a salt mine (point A). Immediately, a lion (point C), a jaguar (point D), and a hyena (point E) demand possession, asserting the rights of the strong. The rabbit, affirming the rights of the weak, makes a fence to isolate the mine from all usurpers.

The required number of rows and columns of dots depended on the tale. To show the marks left by a chased chicken, for example, the drawer would use five rows of six dots. In effect, the Chokwe reduced the memorization of a lusona (singular of sona) to two numbers and a geometric algorithm for constructing one or more curves to create the desired pattern.

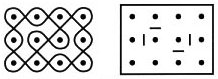
The plaited mat design, where the lines correspond to strands of woven mats, is among the simplest of all sona. In the diagram to the right, try tracing each plaited mat design, making sure you don’t change direction at any intersection. You’ll find that you can create the first figure (left) in one continuous motion but not the second (right), which requires two loops.

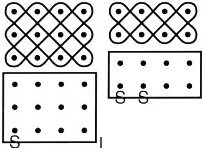
You can imagine that the rectangular arrays are surrounded by mirrored walls. The corresponding sona reflect the paths that light would follow starting near one corner (S in the diagrams, above) and traveling at an angle of 45 degrees and bouncing off the walls.

These simple patterns suggest an interesting mathematical question. Given the number of rows and columns of dots in an array, how many curves does it take to complete a plaited mat design?

When the number of rows equals the number of columns, you would need as many curves as there are rows (or columns). In other words, n curves are required for a plaited mat design on an n by n array.

For a plaited mat design on an m by n rectangular array, you would need as many curves as the greatest common divisor of m and n. So, when m = 3 and n = 4, the greatest common divisor is 1, and only one loop is required. When m = 2 and n = 4, the greatest common divisor is 2, and two loops are required.

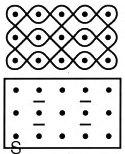
Some sona designs correspond to light-ray patterns created with the addition of horizontal mirrors between the dots. The result is a pattern known as the lion’s stomach. The example shown (right) can be drawn with a single loop.

Mathematician Mark D. Schlatter of Centenary College of Louisiana in Shreveport has analyzed the lion’s stomach pattern and related designs in which only some interior columns of dots have mirrors. He described his findings about how many curves are required for various arrays at the 2001 Bridges meeting, held in July at Southwestern College in Winfield, Kans.

Schlatter looked at permutations–how the numbering of strands changes from one column to the next in a three-row pattern. In an edge column, for instance, the six strands are numbered from 1 to 6 (top to bottom) after they cross. After the next column from the edge, some of the strands would be in different positions relative to the others: for example, 1, 2, 3, 4, 5, and 6 could become 2, 1, 4, 3, 6, and 5.

By studying the permutations that result from different patterns of mirrors acting on strands, Schlatter came up with rules deciding when a generalized lion’s stomach design, which always has an odd number of columns, could be drawn with just a single curve. A three-row array with 4j + 3 columns requires as many curves as rows, he concluded. One with 4j + 1 columns requires only one curve. The example above has 4j + 1 (where j = 1), or 5, columns, so can be drawn with a single curve.

Here’s another generalization that comes out of Schlatter’s work: Any design with an odd number of rows and an odd number of columns with an odd number of horizontal mirrors can’t be drawn as a single loop.

More complicated sona patterns raise new questions. In some cases, for example, the pattern corresponds to the path followed by light reflecting off not only walls and horizontal mirrors but also vertical mirrors. In analyzing these and other patterns, there are many mathematical paths to follow!