There’s more than one way to slice a bagel.
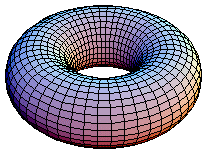
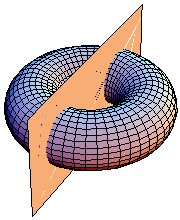
A bagel (or a doughnut) can serve as a physical model for a mathematical surface called a torus. |
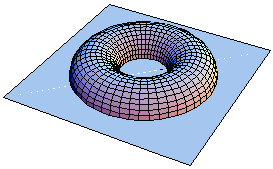
You can slice it horizontally (or longitudinally) so that you end up with two halves, each containing a hole. That’s great for making sandwiches because the cut exposes a reasonably large annular surface on each piece.